安徽省淮北市五校联考 2023-2024学年七年级上学期12月月考数学试题
试卷更新日期:2024-01-16 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 在 , , 0,2这四个数中,最小的一个数是( )A、 B、 C、0 D、22. 圆柱的侧面是( )A、长方形 B、圆形 C、曲面 D、正方形3. 单项式的次数是( )A、2 B、3 C、 D、4. 若方程是关于x的一元一次方程,则a的值为( )A、 B、 C、 D、5. 下列各式中运算正确的是( )A、 B、 C、 D、6. 下列运用等式的性质对等式进行的变形中,不一定正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 若单项式与的和仍是单项式,则方程的解为( )A、 B、 C、 D、8. 有理数 , 在数轴上的位置如图所示,则化简的结果为( )
 A、 B、 C、 D、9. 如图所示的长方形(长为14,宽为8)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( )
A、 B、 C、 D、9. 如图所示的长方形(长为14,宽为8)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( ) A、56 B、40 C、28 D、2010. 定义一种关于整数的“”运算:
A、56 B、40 C、28 D、2010. 定义一种关于整数的“”运算:①当是奇数时,结果为;
②当是偶数时,结果是(其中是使为奇数的正整数),并且运算重复进行.
例如:取 , 第一次经运算是29,第二次经运算是92,第三次经运算是23,第四次经运算是74……若 , 则第2023次经运算的结果是( )
A、6 B、7 C、8 D、9二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 2023年亚运会在杭州市成功举办.据测算,因举办亚运会所增加的投资,对杭州市GDP(国内生产总值)的拉动量约为4141亿元.数据4141亿用科学记数法表示为.12. 如图,用剪刀沿直线将一片平整的圆形纸片剪掉一部分,发现剩下纸片的周长比原纸片的周长要小,能正确解释这一现象的数学知识是.
 13. 若 , 则.14. 我国古代用天干和地支纪年,其中天干有10个:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;地支有12个:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.将天干的10个汉字和地支的12个汉字分别循环排列成如下两行:
13. 若 , 则.14. 我国古代用天干和地支纪年,其中天干有10个:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;地支有12个:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.将天干的10个汉字和地支的12个汉字分别循环排列成如下两行:甲乙丙丁戌己庚辛壬癸甲乙丙丁戌己庚辛壬癸……
子丑寅卯辰巳午未申酉戌亥子丑寅卯辰巳午未申西戌亥……
从左向右第1列是甲子,可以表示甲子年,第4列是丁卯,可以表示丁卯年……
星期
一
二
三
四
五
六
日
与计划量的差值
(1)、在上面的天干排列中,丙第(是正整数)次出现时,是位于从左向右的第列(用含的式子表示);(2)、2023年是癸卯年,癸卯可以位于从左向右的第列(写出一个即可).三、(本大题共2小题,每小题8分,满分16分)
-
15. 计算:(1)、;(2)、.16. 如图,在平面内有 , , 三点.
 (1)、画直线 , 射线 , 线段;(2)、在线段上任取一点(不同于 , ),连接 , 并延长至 , 使.
(1)、画直线 , 射线 , 线段;(2)、在线段上任取一点(不同于 , ),连接 , 并延长至 , 使.四、(本大题共2小题,每小题8分,满分16分)
-
17. 先化简,再求值: , 其中 , .18. 某果农把自家果园的柑橘包装后放到网上销售.原计划每天卖10箱,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某个星期的销售情况(超额记为正,不足记为负,单位:箱).(1)、根据记录的数据可知前五天共卖出多少箱?(2)、本周实际销售总量有没有达到计划数量?请通过计算说明.
五、(本大题共2小题,每小题10分,满分20分)
-
19. 根据经营情况,公司对某商品在甲、乙两地的销售单价进行了如下调整:甲地上涨 , 乙地降价元,已知销售单价调整前甲地比乙地少元,调整后甲地比乙地少元,求调整前甲、乙两地该商品的销售单价.20. 已知点在线段上,点在线段上.
图1
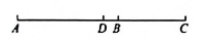 图2
图2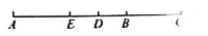 (1)、如图1,若 , , 为线段的中点,求线段的长度;(2)、如图2,若 , 为线段的中点, , 求线段的长度.
(1)、如图1,若 , , 为线段的中点,求线段的长度;(2)、如图2,若 , 为线段的中点, , 求线段的长度.六、(本题满分12分)
-
21. 某服装厂生产一种夹克和T恤,夹克每件定价100元,T恤每件定价50元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款.现某客户要到该服装厂购买夹克30件,T恤件().(1)、若该客户按方案①购买,需付款元(用含的式子表示);若该客户按方案②购买,需付款元(用含的式子表示);(2)、若 , 通过计算说明按①和②哪种方案购买较为合算?(3)、若两种优惠方案可同时使用,当时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
七、(本题满分12分)
-
22. 如图,线段上的点数与线段的总条数有如下关系:
如果线段上有3个点,共有3条线段;
如果线段上有4个点,共有6条线段;
如果线段上有5个点,共有10条线段.
 (1)、当线段上有6个点时,共有多少条线段?(2)、当线段上有个点时,共有多少条线段?(用含的代数式表示)(3)、当时,共有多少条线段?
(1)、当线段上有6个点时,共有多少条线段?(2)、当线段上有个点时,共有多少条线段?(用含的代数式表示)(3)、当时,共有多少条线段?八、(本题满分14分)
-
23. 对于数轴上的点 , 线段 , 给出如下定义:
为线段上任意一点,我们把 , 两点间距离的最小值称为点关于线段的“靠近距离”,记作(点 , 线段);把 , 两点间的距离的最大值称为点关于线段的“远离距离”,记作(点 , 线段).若点与点重合,则 , 两点间的距离为0.
如图,已知点表示的数为 , 点表示的数为2.
若点表示的数为3,则(点 , 线段) , (点.线段).
 (1)、若点表示的数为 , 则(点 , 线段) , (点 , 线段);(2)、若点表示的数为 , (点 , 线段) , 则的值为;若点表示的数为 , (点 , 线段) , 则的值为;(3)、若点表示的数为 , 点表示的数为 , (点 , 线段)是(点 , 线段)的3倍.求的值.
(1)、若点表示的数为 , 则(点 , 线段) , (点 , 线段);(2)、若点表示的数为 , (点 , 线段) , 则的值为;若点表示的数为 , (点 , 线段) , 则的值为;(3)、若点表示的数为 , 点表示的数为 , (点 , 线段)是(点 , 线段)的3倍.求的值.
-
-