安徽省亳州市2023-2024学年八年级上学期第三次月考数学试题

试卷更新日期：2024-01-16 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，满分40分）

1. 在平面直角坐标系中，点 $A (- 4 ， 3)$ 到 $x$ 轴的距离是（）

A、4 B、3 C、 $- 4$ D、 $- 3$

查看试题解析
2. 下列图形中，最具有稳定性质的是（）

A、 B、 C、 D、

查看试题解析
3. 一次函数 $y = a x - 3$ 的值随 $x$ 的增大而减小；则点 $P (3 ， a)$ 所在象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图， $△ A B C ≌ △ D E F$ ，点 $B ， E ， C ， F$ 共线，已知 $∠ B = 40 ° ， ∠ D = 80 °$ ，则 $∠ A C F$ 的度数为（）

A、 $135 °$ B、 $125 °$ C、 $120 °$ D、 $100 °$

查看试题解析
5. 如图，在平面直角坐标系，线段 $A B$ 的两个端点坐标依次为 $A (- 2 ， - 1) ， B (- 2 ， 2)$ ，将线段 $A B$ 向右平移5个单位，再向上平移1个单位，得到对应线段 $C D$ ，则四边形 $A B D C$ 的面积为（）

A、7.5 B、10.5 C、15 D、18

查看试题解析
6. 一次函数 $y = - 2 x + 1$ 中，当 $- 1 \leq x \leq 3$ 时，则函数 $y$ 的取值范围为（）

A、 $3 \leq y \leq 5$ B、 $- 5 \leq y \leq 3$ C、 $- 3 \leq y \leq 5$ D、 $- 3 \leq y \leq 3$

查看试题解析
7. 下列条件能确定 $△ A B C$ 的形状与大小的是（）

A、 $∠ A = 20 ° ， ∠ B = 70 ° ， ∠ C = 90 °$ B、 $A B = A C ， B C = 6$ C、 $A B = 10 ， A C = 8 ， ∠ A B C = 30 °$ D、 $∠ A = 90 ° ， B C = 5 ， A B = 2$

查看试题解析
8. 如图是一个不规则的“五角星”，已知 $∠ A = 54 ° ， ∠ C = 40 ° ， ∠ D = 32 ° ， ∠ B = ∠ E$ ，则 $∠ B$ 的度数为（）

A、 $27 °$ B、 $30 °$ C、 $34 °$ D、 $40 °$

查看试题解析
9. 在同一直角坐标系中，一次函数 $y = m x + n$ （ $m$ 和 $n$ 是常数）与 $y = n x + m$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 在 $△ A B C$ 中， $A C > A B$ ，点 $D$ 是 $B C$ 边的中点，过点 $B$ 作 $B E ⊥ A D$ 于点 $E$ ，点 $F$ 是 $D A$ 延长线上一点，已知 $∠ B F D = ∠ C A D$ ，下列结论不一定正确的是（）

A、 $B F = A C$ B、 $A E = B E$ C、 $A F = 2 D E$ D、 $S_{△ B E F} = S_{△ B D E} + S_{△ A C D}$

查看试题解析

二、填空题（本大题共4小题，每小题5分，满分20分）

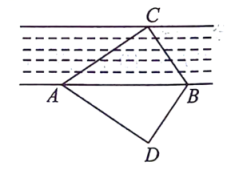
11. 把命题“全等三角形的对应高线相等”改写成“如果……，那么……．的形式：．

查看试题解析
12. 在平面直角坐标系中，已知点 $P (- 1 ， - 3)$ 和 $Q (3 a + 1 ， 3 - 2 a)$ ，且 $P Q ∥ x$ 轴，则 $a$ 的值为．

查看试题解析
13. 某数学兴趣小组利用全等三角形的知识测试某小河的宽度，如图，点 $A ， B ， C$ 是小河两边的三点，在河边 $A B$ 下方选择一点，使得 $∠ B A D = ∠ B A C ， ∠ A B D = ∠ A B C$ ，若测得 $A B = 10$ 米， $△ A B D$ 的面积为30平方米，则点 $C$ 到 $A B$ 的距离为米．

查看试题解析
14. 已知一次函数 $y = a x + 8 - 2 a$ （ $a$ 为常数且 $a \neq 0$ ）．

(1)、若该一次函数图象经过点 $(- 1 ， 2)$ ，则 $a =$ ；

(2)、当 $- 2 \leq x \leq 5$ 时，函数 $y$ 有最大值11，则 $a$ 的值为．

查看试题解析

三、（本大题共2小题，每小题8分，满分16分）

15. 如图，已知 $A B = A C ， B D = C D$ ，证明： $∠ B = ∠ C$ ．

查看试题解析
16. 已知一次函数的图象与正比例函数 $y = - \frac{1}{2} x$ 的图象平行且经过点 $(4 ， 1)$ ，求该一次函数的表达式．

查看试题解析

四、（本大题共2小题，每小题8分，满分16分）

17. 如图，在平面直角坐标系 $x O y$ 中，点 $A$ 和点 $B$ 的坐标分别为 $(- 3 ， 3) ， (- 3 ， - 1)$ ．

(1)、将 $△ A O B$ 向右平移4个单位，再向下平移2个单位，得到 $△ A_{1} O_{1} B_{1}$ ，画出 $△ A_{1} O_{1} B_{1}$ ；

(2)、用无刻度直尺在网格内画出 $△ A C B$ ，使得 $△ A O B ≌ △ B C A$ ，并写出点 $C$ 的坐标．

查看试题解析
18. 如图，在 $△ A B C$ 和 $△ A D E$ 中，点 $C$ 和点 $E$ 分别是 $A D$ 和 $A B$ 上的点， $D E$ 与 $B C$ 交于点 $F$ ，已知 $∠ A C B = ∠ A E D ， B C = D E$ ．

(1)、证明： $B E = D C$ ；

(2)、若 $∠ A = 40 ° ， ∠ B = 32 °$ ，求 $∠ B F D$ 的度数．

查看试题解析

五、（本大题共2小题，每小题10分，满分20分）

19. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点 $D$ ，点 $E$ 是 $A D$ 上一点，连接 $C E$ 并延长交 $A B$ 于点 $F$ ，已知 $A B = C E ， B D = E D$ ．

(1)、证明： $C E ⊥ A B$ ；

(2)、若 $B D = 2 ， C D = 5$ ，求 $△ A C E$ 的面积．

查看试题解析
20. 某种中性笔在甲、乙两家文具店的标价都是4元/支，在“双11”期间，两家文具店都进行了优惠活动．甲文具店：购买不超过20支按原价销售，超出20支的部分按6折销售；乙文具店：不论买多少，全部按八折销售．

(1)、分别写出甲、乙两家文具店购买这种中性笔所付总费用 $y_{甲} 、 y_{乙}$ （元）与购买支数 $x (x > 20)$ 之间的函数表达式；

(2)、若某学校购买50枝这种中性笔，请你通过计算说明在哪家文具店购买划算．

查看试题解析

六、（本题满分12分）

21. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点 $D ， A E$ 平分 $∠ B A C$ 交 $B C$ 于点 $E$ ．
图1 图2

(1)、若 $∠ B = 80 ° ， ∠ C = 28 °$ ，如图1，求 $∠ D A E$ 的度数；

(2)、若 $∠ B A C = ∠ B = 2 ∠ C$ ，如图2，证明： $△ A B D ≌ △ A E D$ ．

查看试题解析

七、（本题满分12分）

22. 如图，直线 $l_{1} ： y_{1} = k_{1} x (k_{1} \neq 0)$ 与直线 $l_{2} ： y_{2} = k_{2} x + b (k_{2} \neq 0)$ 交于点 $C (- 2 ， 3)$ ，直线 $l_{2}$ 与 $x$ 轴、 $y$ 轴分别交于点 $A ， B (0 ， 4)$ ．

(1)、求 $k_{1} ， k_{2} ， b$ 的值；

(2)、直接写出不等式组 $k_{2} x + b \geq k_{1} x \geq 0$ 的解集：；

(3)、点 $P$ 是直线 $l_{2}$ 上一点，且满足 $S_{△ A O P} = 2 S_{△ B O C}$ ，求点 $P$ 的坐标．

查看试题解析

八、（本题满分14分）

23. 如图，在 $△ A B C$ 中， $∠ A B C = 90 ° ， A B = B C ， ∠ A C B = 45 °$ ，点 $A$ 和点 $B$ 分别落在 $y$ 轴的正半轴和 $x$ 轴的正半轴上，已知点 $C$ 的坐标为 $(- 2 ， - 2)$ ．
图1 图2 图3

(1)、如图1，过点 $C$ 作 $C D ⊥ x$ 轴于点 $D$ ，证明： $△ B C D ≌ △ A B O$ ，并直接写出点 $A$ 的坐标；

(2)、如图2，若 $B C$ 与 $y$ 轴交于点 $E$ ，证明： $A E$ 是 $△ A B C$ 的中线；

(3)、如图3，若 $A C$ 与 $x$ 轴交于点 $F$ ，连接 $E F$ ，探索线段 $A E ， E F$ 和 $B F$ 之间的数量关系，并加以证明．

查看试题解析