广西壮族自治区河池市凤山县2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-01-16 类型:期末考试
一、选择题(共12小题,每小题3分,共36分.)
-
1. 下列式子中是分式的是( )A、2 B、 C、 D、2. 在下列各组图形中,属于全等图形的是( )A、

 B、
B、
 C、
C、
 D、
D、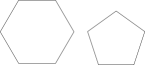 3. 如图,人字梯中间一般会设计一“拉杆”,这样做的道理是( )
3. 如图,人字梯中间一般会设计一“拉杆”,这样做的道理是( ) A、三角形具有稳定性 B、垂线段最短 C、两点之间,线段最短 D、两直线平行,内错角相等4. 石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为0.000000000142米 ,数字“0.000000000142”用科学记数法表示为( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A、6 B、7 C、8 D、97. 如果是一个完全平方式,则的值是( )A、3 B、 C、3或 D、6或8. 如图, , 若 , 则的度数是( )
A、三角形具有稳定性 B、垂线段最短 C、两点之间,线段最短 D、两直线平行,内错角相等4. 石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为0.000000000142米 ,数字“0.000000000142”用科学记数法表示为( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A、6 B、7 C、8 D、97. 如果是一个完全平方式,则的值是( )A、3 B、 C、3或 D、6或8. 如图, , 若 , 则的度数是( ) A、 B、 C、 D、9. 如图,在中,点D是AC的中点,分别以点A , C为圆心,大于的长为半径作弧,两弧交于F , 直线FD交BC于点E , 连接AE , 若 , 的周长为12,则的周长为( )
A、 B、 C、 D、9. 如图,在中,点D是AC的中点,分别以点A , C为圆心,大于的长为半径作弧,两弧交于F , 直线FD交BC于点E , 连接AE , 若 , 的周长为12,则的周长为( ) A、13 B、14 C、15 D、1610. 等腰三角形一腰上的高与另一腰上的夹角为 , 则顶角的度数为( )A、 B、 C、或 D、或11. 计算的结果等于( )A、1 B、 C、 D、12. 如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )个.
A、13 B、14 C、15 D、1610. 等腰三角形一腰上的高与另一腰上的夹角为 , 则顶角的度数为( )A、 B、 C、或 D、或11. 计算的结果等于( )A、1 B、 C、 D、12. 如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )个. A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题(本大题共6小题,每小题2分,共12分.)
-
13. 使分式有意义的x的取值范围是 .14. 已知 , , 则的值为 .15. 如图,在中, , 点B在第四象限时,则点B的坐标为 .
 16. 如图,将透明直尺叠放在正五边形徽章上,若直尺的一边于点O , 且经过点B , 另一边经过点E , 则的度数为 .
16. 如图,将透明直尺叠放在正五边形徽章上,若直尺的一边于点O , 且经过点B , 另一边经过点E , 则的度数为 . 17. 如图, , , 点在的垂直平分线上,若 , 则为.
17. 如图, , , 点在的垂直平分线上,若 , 则为. 18. 如图,在四边形中, , , 在 , 上分别找一个点M , N , 使的周长最小,则°
18. 如图,在四边形中, , , 在 , 上分别找一个点M , N , 使的周长最小,则°
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 计算: .20. 先化简,再求值: , 其中 .21. 如图,在由边长为个单位的小正方形组成的网格中,三角形的顶点均为格点(网格线的交点).
 (1)、作出三角形关于直线的轴对称图形三角形;(2)、求三角形的面积;(3)、在直线上找一点使得三角形的面积等于三角形的面积.22. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.
(1)、作出三角形关于直线的轴对称图形三角形;(2)、求三角形的面积;(3)、在直线上找一点使得三角形的面积等于三角形的面积.22. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.

活动前骑电瓶车戴安全帽情况统计表
类别
人数
A
68
B
245
C
510
D
177
合计
1000
(1)、宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?(2)、该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;(3)、小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.23. (1)、如图1,若大正方形的边长为 , 小正方形的边长为 , 则阴影部分的面积是;若将图1中的阴影部分裁剪下来,重新拼成如图2的一个长方形,则它的长为;宽为;面积为 .(2)、由(1)可以得到一个公式: .(3)、利用你得到的公式计算: .24. 如图,中,点D在边上, , 的平分线交于点E , 过点E作 , 垂足为 , 且 , 连接 .
(1)、如图1,若大正方形的边长为 , 小正方形的边长为 , 则阴影部分的面积是;若将图1中的阴影部分裁剪下来,重新拼成如图2的一个长方形,则它的长为;宽为;面积为 .(2)、由(1)可以得到一个公式: .(3)、利用你得到的公式计算: .24. 如图,中,点D在边上, , 的平分线交于点E , 过点E作 , 垂足为 , 且 , 连接 . (1)、求证:平分;(2)、若 , 求的面积.25. 某商场准备购进甲、乙两种商品进行销售,若每个甲商品的进价比每个乙商品的进价少2元,且用80元购进甲商品的数量与用100元购进乙商品的数量相同.(1)、甲、乙两种商品每个的进价分别是多少元?(2)、若该商场购进甲商品的数量比购进乙商品的数量的3倍还少5个,且购进甲、乙两种商品的总数量不超过95个,则商场最多购进乙商品多少个?(3)、在(2)的条件下,如果甲、乙两种商品的售价分别是12元/个和15元/个,且将购进的甲、乙两种商品全部售出后,可使销售两种商品的总利润超过380元,那么该商场购进甲、乙两种商品有哪几种方案?26. 如图,在等边中,点D , E分别在边上,且 与相交于点P , 于点Q
(1)、求证:平分;(2)、若 , 求的面积.25. 某商场准备购进甲、乙两种商品进行销售,若每个甲商品的进价比每个乙商品的进价少2元,且用80元购进甲商品的数量与用100元购进乙商品的数量相同.(1)、甲、乙两种商品每个的进价分别是多少元?(2)、若该商场购进甲商品的数量比购进乙商品的数量的3倍还少5个,且购进甲、乙两种商品的总数量不超过95个,则商场最多购进乙商品多少个?(3)、在(2)的条件下,如果甲、乙两种商品的售价分别是12元/个和15元/个,且将购进的甲、乙两种商品全部售出后,可使销售两种商品的总利润超过380元,那么该商场购进甲、乙两种商品有哪几种方案?26. 如图,在等边中,点D , E分别在边上,且 与相交于点P , 于点Q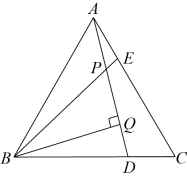 (1)、求证:;(2)、求的度数;(3)、若 , 求的长.
(1)、求证:;(2)、求的度数;(3)、若 , 求的长.