陕西省榆林市榆阳区2023-2024学年八年级上册数学期末考试试卷
试卷更新日期:2024-01-16 类型:期末考试
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题目要求的)
-
1. 下列四个实数中,最大的数是( )A、 B、2 C、0 D、
-
2. 下列各组数中,以它们为边长能构成直角三角形的是( )A、2,3,4 B、1,2, C、2,2, D、 , ,
-
3. 如图,直线 , 直线与直线a相交于点P , 与直线b相交于点Q , 于点P , 若 , 则的度数为( )
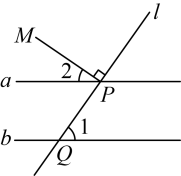 A、 B、 C、 D、
A、 B、 C、 D、 -
4. 甲、乙、丙、丁四名运动员进行百米测试,每人8次测试成绩的平均数都是秒,方差分别为 , , , , 则这四名运动员百米成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁
-
5. 如图,在Rt△ABC中, , 正方形AEDC , BCFG的面积分别为25和144,则AB的长度为( )
 A、13 B、169 C、119 D、
A、13 B、169 C、119 D、 -
6. 下列命题中,是真命题的是( )A、同位角相等 B、若 , 则 C、垂线段最短 D、过两点可以画很多条直线
-
7. 在平面直角坐标系中,若 , , 则一次函数的图象大致是( )A、
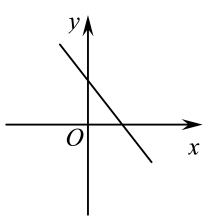 B、
B、 C、
C、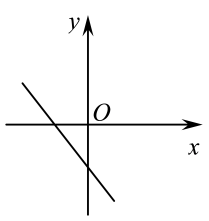 D、
D、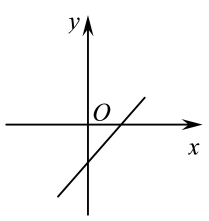
-
8. 如图,添加下列一个条件后,能判定的是( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题(共5小题,每小题3分,计15分)
-
9. 计算: .
-
10. 如图,已知是的外角, , , 则的度数为 .

-
11. 若是方程的一个解,则的值为 .
-
12. 如图,直线与直线相交于点 , 则关于x , y二元一次方程组的解为 .

-
13. 如图,在长方形中, , , 点为边上的一个动点,把沿折叠,若点的对应点刚好落在边上,则的长为 .

三、解答题(共13小题,计81分.解答应写出过程)
-
14. 计算: .
-
15. 解方程组
-
16. 学校为了解本校学生对我国航天科技及空间站的知晓情况,在全校开展了“中国梦•航天情”系列活动,从知识竞赛,演讲比赛,制作宣传海报三个方面对全校学生进行考察,下面是张晓同学各项目的成绩,如果将知识竞赛,演讲比赛,制作宣传海报这三项得分依次按 , , 的比例计算学生的成绩,求张晓同学的最终成绩.
项目
知识竞赛
演讲比赛
制作宣传海报
成绩/分
92
90
80
-
17. 甘肃地震牵动全国,甲、乙两人沿同一条路用货车从地匀速开往相距的灾区地运送救灾物资.如图,和分别表示甲、乙与地的距离与行驶的时间之间的关系.
 (1)、甲出发后,两人相遇,这时他们与地的距离为;(2)、甲的速度是 , 乙的速度是;(3)、乙从地出发时到达地.
(1)、甲出发后,两人相遇,这时他们与地的距离为;(2)、甲的速度是 , 乙的速度是;(3)、乙从地出发时到达地. -
18. 如图,在中,CD是的角平分线,点E在AC上, , 若 , , 求的度数.
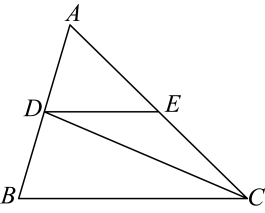
-
19. 如图,在平面直角坐标系中,顶点的坐标分别为 , , .
 (1)、请画出关于轴对称的 , 点的对应点分别为 , , ;(2)、请写出点 , 的坐标:( , ),( , ).
(1)、请画出关于轴对称的 , 点的对应点分别为 , , ;(2)、请写出点 , 的坐标:( , ),( , ). -
20. 风陵渡黄河公路大桥是连接山西、陕西、河南三省的交通要塞,该大桥限重标志牌显示,载重后总质量超过30吨的车辆禁止通行,现有一辆自重8吨的卡车,要运输若干套某种设备,每套设备由1个A部件和3个B部件组成,这种设备必须成套运输,已知1个A部作和2个B部件的总质量为2.8吨,2个A部件和3个B部件的质量相等,1个A部件和1个B部件的质量各是多少吨?
-
21. 如图,一棵竖直的大杉树在一次台风中被刮断 , 树顶落在离树根处,工作人员要查看断痕处的情况,在离树根有的处架起一个长的梯子 , 点在同一条直线上,求这棵树原来的总高度.
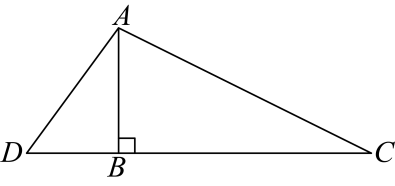
-
22. 为了倡导“节约用水,从我做起”,市政府决定对某小区户家庭的用水情况进行调查,调查小组随机抽查了其中户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
 (1)、这次调查结果的中位数为吨,众数为吨;(2)、求这次调查结果的平均数;(3)、根据上述调查结果,估计该小区户家庭中月平均用水量超过12吨的约有多少户?
(1)、这次调查结果的中位数为吨,众数为吨;(2)、求这次调查结果的平均数;(3)、根据上述调查结果,估计该小区户家庭中月平均用水量超过12吨的约有多少户? -
23. 某种商品每件的进价为10元,若每件按20元的价格销售,则每月能卖出360件;若每件按30元的价格销售,则每月能卖出60件,假定每月的销售件数y(件)是每件商品销售价格x(元)的一次函数,且 .(1)、求每月的销售件数y(件)关于每件商品销售价格x(元)的函数表达式;(2)、若要使这种商品每月销售件数是300件,每件商品的销售价格应定为多少元?
-
24. 如图, , 点是的延长线上的一点,交于点 , , , .
 (1)、求证:;(2)、若 , , 求的度数.
(1)、求证:;(2)、若 , , 求的度数. -
25. 某车间有50名工人,每人每天可加工16个甲种零件或15个乙种零件,安排其中一部分工人加工甲种零件,其余工人加工乙种零件,已知每加工一个甲种零件可获利20元,每加工一个乙种零件可获利24元.(1)、若该车间某天获利17000元,问这天加工甲种零件的工人多少人?(2)、由于生产需要,每天都需要加工两种零件,设加工甲种零件的人数为m .
①请用含m的式子表示该车间每天的获利w(元);
②若 , 求当m为何值时,该车间一天的获利w最大?最大为多少元?
-
26. 如图①,直线与轴交于点 , 与轴交于点 , 与直线交于点 .
 (1)、直接写出点的坐标:( , ),( , );(2)、点是轴上一点,若的面积为6,求点的坐标;(3)、如图②,过轴正半轴上的动点作直线轴,点在直线上,若以为顶点的三角形是等腰直角三角形,请求出的值.
(1)、直接写出点的坐标:( , ),( , );(2)、点是轴上一点,若的面积为6,求点的坐标;(3)、如图②,过轴正半轴上的动点作直线轴,点在直线上,若以为顶点的三角形是等腰直角三角形,请求出的值.
