黑龙江哈尔滨市香坊区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-01-16 类型:期末考试
一、选择题(每题3分,共计30分)
-
1. 若点是反比例函数图象上一点,则常数的值为( )A、3 B、 C、 D、2. 下列图形中,只是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 将抛物线 向右平移3个单位,再向上平移4个单位,得到的抛物线是( )A、 B、 C、 D、4. 如图是用5个相同的立方体搭成的几何体,其俯视图是( )
3. 将抛物线 向右平移3个单位,再向上平移4个单位,得到的抛物线是( )A、 B、 C、 D、4. 如图是用5个相同的立方体搭成的几何体,其俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 在中, , , , 则的值是( )A、5 B、 C、4 D、6. 在一个不透明的袋子中有2个红球,3个绿球和4个蓝球,它们只有颜色上的区别,若从袋子里随机取出一球,则取出这个球是绿球的概率为( )A、 B、 C、 D、7. 如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
5. 在中, , , , 则的值是( )A、5 B、 C、4 D、6. 在一个不透明的袋子中有2个红球,3个绿球和4个蓝球,它们只有颜色上的区别,若从袋子里随机取出一球,则取出这个球是绿球的概率为( )A、 B、 C、 D、7. 如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )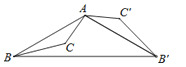 A、45° B、60° C、70° D、90°8. 如图,四边形内接于为对角线,经过圆心 . 若 , 则的度数为( )
A、45° B、60° C、70° D、90°8. 如图,四边形内接于为对角线,经过圆心 . 若 , 则的度数为( )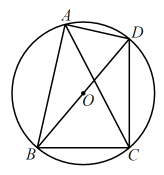 A、 B、 C、 D、9. 如图,已知 , , 则下列比例中错误的是( )
A、 B、 C、 D、9. 如图,已知 , , 则下列比例中错误的是( ) A、 B、 C、 D、10. 如图,抛物线与轴交于点 , 其对称轴为直线 , 结合图象给出下列结论:①;②;③;④ , 其中正确的结论有( )
A、 B、 C、 D、10. 如图,抛物线与轴交于点 , 其对称轴为直线 , 结合图象给出下列结论:①;②;③;④ , 其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共计30分)
-
11. 在平面直角坐标系中,点关于原点对称的点的坐标为.12. 已知二次函数的顶点坐标为.13. 若点 , 在反比例函数的图象上,则 , 的大小关系用“<”连接的结果为.14. 如图,设在小孔口前处有一支长的蜡烛 , 经小孔形成的像 , 恰好照在距小孔后面处的屏幕上,则像的长.
 15. 如图,是的切线,切点为 , 的延长线交于点 , 若 , 则的度数为.
15. 如图,是的切线,切点为 , 的延长线交于点 , 若 , 则的度数为. 16. 如图,是操场上直立的一个旗杆,旗杆上有一点 , 用测角仪(测角仪的高度忽略不计)测得地面上的点到点的仰角 , 到点的仰角 , 若米,则旗杆的高度米.
16. 如图,是操场上直立的一个旗杆,旗杆上有一点 , 用测角仪(测角仪的高度忽略不计)测得地面上的点到点的仰角 , 到点的仰角 , 若米,则旗杆的高度米. 17. 某学习小组由1名男生和3名女生组成,在一次合作学习中,若随机抽取2保同学汇报展示,则抽到1名男生和1名女生的概率为.18. 一个扇形的圆心角为 , 弧长为 , 则此扇形的面积是.19. 在矩形中,点在直线上, , 若 , , 则的正切值为.20. 如图1,在中, , 是上一点,过点作交于 , 将绕点顺时针旋转到图2的位置,若 , , 则线段的长为.
17. 某学习小组由1名男生和3名女生组成,在一次合作学习中,若随机抽取2保同学汇报展示,则抽到1名男生和1名女生的概率为.18. 一个扇形的圆心角为 , 弧长为 , 则此扇形的面积是.19. 在矩形中,点在直线上, , 若 , , 则的正切值为.20. 如图1,在中, , 是上一点,过点作交于 , 将绕点顺时针旋转到图2的位置,若 , , 则线段的长为.
三、解答题(共计60分)
-
21. 先化简,再求代数式的值,其中.22. 如图所示,在平面直角坐标系中,为坐标原点,的各顶点坐标分别为 , , .
 (1)、画出关于原点中心对称的图形;(2)、将绕点顺时针旋转得到 , 请画出;(3)、连接并直接写出线段的长.23. 如图,某座山的主峰观景平台高450米,登山者需由山底处先步行300米到达处,再由处乘坐登山缆车到达观景平台处.已知点 , , , , , 在同一平面内, , 于 , 山坡的坡角为 , 缆车行驶路线与水平面的夹角为(换乘登山缆车的时间忽略不计).
(1)、画出关于原点中心对称的图形;(2)、将绕点顺时针旋转得到 , 请画出;(3)、连接并直接写出线段的长.23. 如图,某座山的主峰观景平台高450米,登山者需由山底处先步行300米到达处,再由处乘坐登山缆车到达观景平台处.已知点 , , , , , 在同一平面内, , 于 , 山坡的坡角为 , 缆车行驶路线与水平面的夹角为(换乘登山缆车的时间忽略不计). (1)、求登山缆车上升的高度;(2)、若小明步行速度为 , 登山缆车的速度为 , 求小明从山底处到达山顶处大约需要多少分钟(结果精确到).(参考数据: , , )24. 如图,、、都是的半径,.
(1)、求登山缆车上升的高度;(2)、若小明步行速度为 , 登山缆车的速度为 , 求小明从山底处到达山顶处大约需要多少分钟(结果精确到).(参考数据: , , )24. 如图,、、都是的半径,. (1)、求证:;(2)、若 , , 求的半径.25. 把边长为的正方形硬纸板(如图1),在四个顶点处分别剪掉一个小正方形,折成一个长方体形的无盖盒子(如图2),折纸厚度忽略不计.
(1)、求证:;(2)、若 , , 求的半径.25. 把边长为的正方形硬纸板(如图1),在四个顶点处分别剪掉一个小正方形,折成一个长方体形的无盖盒子(如图2),折纸厚度忽略不计.
图1图2
(1)、要使折成的盒子的底面积为 , 剪掉的正方形边长应是多少厘米?(2)、折成的长方体盒子侧面积(四个侧面的面积之和)有没有最大值?如果没有,说明理由:如果有,求出这个最大值,并求出此时剪掉的正方形边长.26. 菱形中,对角线、相交于点 , , 点为上一点,点为上一点,连接 , 将线段绕点顺时针旋转得到对应线段 , 连接.
图1 图2

图3 图4
(1)、当点与点重合时:①如图1,点落在对角线上,则线段、之间的数量关系为_▲_;
②如图2,点不落在对角线上,则①问中结论是否成立,为什么?
(2)、当点与点不重合时:①如图3,点不落在对角线上,则(1)问中结论,_▲_;(填“成立”或“不成立”)
②如图4,在①的条件下,延长交于点 , 交于点 , 若 , , , 求线段的长.
27. 如图,在平面直角坐标系中,点为坐标原点,抛物线交轴负半轴于点 , 交轴正半轴于点 , 交轴于点 , 直线经过点 , 并抛物线于点. (1)、如图1,求抛物线解析式;(2)、如图2,为抛物线第四象限上一点,连接、 , 设点的横坐标为,的面积为 , 求与之间的函数关系式,并直接写出自变量的取值范围;(3)、如图3,在(2)的条件下,过点作交轴于点 , 垂足为点 , 为抛物线第二象限上一点,连接 , , 过点作轴交于点 , 若 , 求的值及点坐标.
(1)、如图1,求抛物线解析式;(2)、如图2,为抛物线第四象限上一点,连接、 , 设点的横坐标为,的面积为 , 求与之间的函数关系式,并直接写出自变量的取值范围;(3)、如图3,在(2)的条件下,过点作交轴于点 , 垂足为点 , 为抛物线第二象限上一点,连接 , , 过点作轴交于点 , 若 , 求的值及点坐标.