广东省惠州市惠城区2023-2024学年九年级(上)期末考试模拟卷数学试题
试卷更新日期:2024-01-16 类型:期末考试
一、选择题(共10小题,满分30分,每小题3分)
-
1. 下列图案中是中心对称图形的是( )A、
 B、
B、 C、
C、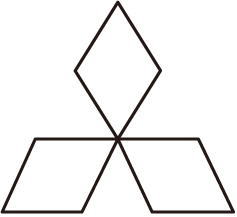 D、
D、 2. 一元二次方程x2+2x﹣3=0配方后可化为( )A、(x﹣1)2=2 B、(x+1)2=2 C、(x﹣1)2=4 D、(x+1)2=43. 下列事件是随机事件的是( )A、任意画一个三角形,该三角形的内角和为180° B、任意取出两个正数,这两个正数的和为负数 C、从分别写有2,4,6的三张卡片中随机抽出一张,卡片上的数字能被2整除 D、任意抛掷一枚质地均匀的硬币,正面向上4. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
2. 一元二次方程x2+2x﹣3=0配方后可化为( )A、(x﹣1)2=2 B、(x+1)2=2 C、(x﹣1)2=4 D、(x+1)2=43. 下列事件是随机事件的是( )A、任意画一个三角形,该三角形的内角和为180° B、任意取出两个正数,这两个正数的和为负数 C、从分别写有2,4,6的三张卡片中随机抽出一张,卡片上的数字能被2整除 D、任意抛掷一枚质地均匀的硬币,正面向上4. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )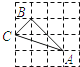 A、
A、 B、
B、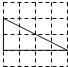 C、
C、 D、
D、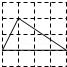 5. 如图,AB为⊙O的直径,C , D为⊙O上的点, . 若∠CBD=35°,则∠ABD的度数为( )
5. 如图,AB为⊙O的直径,C , D为⊙O上的点, . 若∠CBD=35°,则∠ABD的度数为( ) A、20° B、35° C、40° D、70°6. 已知点A(﹣2,y1)、B(1,y2)、C(3,y3)三点都在反比例函数y=(k<0)的图象上,则下列关系正确的是( )A、y2<y3<y1 B、y3<y2<y1 C、y1<y3<y2 D、y1<y2<y37. 若y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为( )
A、20° B、35° C、40° D、70°6. 已知点A(﹣2,y1)、B(1,y2)、C(3,y3)三点都在反比例函数y=(k<0)的图象上,则下列关系正确的是( )A、y2<y3<y1 B、y3<y2<y1 C、y1<y3<y2 D、y1<y2<y37. 若y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为( )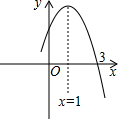 A、﹣2 B、﹣1 C、0 D、18. 据国家统计局发布的《2022年国民经济和社会发展统计公报》显示,2020年和2022年全国居民人均可支配收入分别为3.2万元和3.7万元.设2020年至2022年全国居民人均可支配收入的年平均增长率为x , 依题意可列方程为( )A、3.2(1﹣x)2=3.7 B、3.2(1+x)2=3.7 C、3.7(1﹣x)2=3.2 D、3.7(1+x)2=3.29. 如图,△ABC是等边三角形,被一矩形所截,AB被截成三等分,EH∥BC , 则四边形EFGH的面积是△ABC的面积的( )
A、﹣2 B、﹣1 C、0 D、18. 据国家统计局发布的《2022年国民经济和社会发展统计公报》显示,2020年和2022年全国居民人均可支配收入分别为3.2万元和3.7万元.设2020年至2022年全国居民人均可支配收入的年平均增长率为x , 依题意可列方程为( )A、3.2(1﹣x)2=3.7 B、3.2(1+x)2=3.7 C、3.7(1﹣x)2=3.2 D、3.7(1+x)2=3.29. 如图,△ABC是等边三角形,被一矩形所截,AB被截成三等分,EH∥BC , 则四边形EFGH的面积是△ABC的面积的( )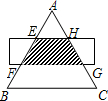 A、 B、 C、 D、10. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的一个交点为(﹣1,0),对称轴为直线x=2.则下列结论:
A、 B、 C、 D、10. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的一个交点为(﹣1,0),对称轴为直线x=2.则下列结论:
①abc>0;
②a+2c<﹣b;
③c﹣3a=0;
④直线y=m可能与y=|ax2+bx+c|有4个交点;
⑤若点M(x1 , y2),点N(x1 , y2)是抛物线上的两点,若x1<x2 , 则y1<y2 .
其中正确的有( )
A、2个 B、3个 C、4个 D、5个二、填空题(共6小题,满分18分,每小题3分)
-
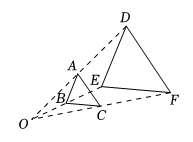
11. 抛物线y=(x﹣2)2+2的顶点坐标是 .12. 已知点P(x , ﹣2)与点Q(4,y)关于原点对称,则x+y的值是 .13. 已知关于x的方程x2+kx﹣10=0的一个根是2,则k= .14. 如图,△ABC与△DEF位似,点O为位似中心,已知OA:OD=1:2,则△ABC与△DEF的周长之比为 .
 15. 如图,△ABC是⊙O的内接正三角形,图中阴影部分的面积是12π,则⊙O的半径为 .
15. 如图,△ABC是⊙O的内接正三角形,图中阴影部分的面积是12π,则⊙O的半径为 .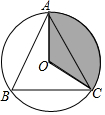 16. 如图,点A在反比例函数的图象上,AB⊥x轴于点B , C是OB的中点,连接AO , AC , 若△AOC的面积为4,则k= .
16. 如图,点A在反比例函数的图象上,AB⊥x轴于点B , C是OB的中点,连接AO , AC , 若△AOC的面积为4,则k= .
三、解答题(共9小题,满分72分)
-
17. 解方程:x2﹣4x+3=0.18. 如图,在平面直角坐标系中,的三个顶点分别是 , , .
 (1)、在图中画出 , 使得与关于点对称;(2)、在(1)的基础上,画出绕点逆时针旋转后的 , 并直接写出点的坐标.19. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的 , , , 四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到小区的概率是 ;(2)、请用列表或画树状图的方法求甲组抽到小区,同时乙组抽到小区的概率.20. 如图,一次函数y=ax+b的图象与反比例函数的图象交于M(﹣1,﹣4)、N(2,m)两点.
(1)、在图中画出 , 使得与关于点对称;(2)、在(1)的基础上,画出绕点逆时针旋转后的 , 并直接写出点的坐标.19. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的 , , , 四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到小区的概率是 ;(2)、请用列表或画树状图的方法求甲组抽到小区,同时乙组抽到小区的概率.20. 如图,一次函数y=ax+b的图象与反比例函数的图象交于M(﹣1,﹣4)、N(2,m)两点. (1)、求反比例函数和一次函数的解析式;(2)、求△MON的面积.21. “十一”期间,某花店以每盆20元的价格购进一批花卉、市场调查反映:该花卉每盆售价25元时,每天可卖出25盆、若涨价销售,每盆花卉每涨价1元,每天要少卖出1盆.(1)、若该花卉每天的销售利润为200元,且销量尽可能大,每盆花卉售价是多少元?(2)、为了让利给顾客,该花店决定每盆花卉涨价不超过6元,问该花卉一天最大的销售利润是多少元?22. 如图,正方形ABCD与正方形AEFG的边长分别为和2,现在将正方形AEFG绕着点A旋转.
(1)、求反比例函数和一次函数的解析式;(2)、求△MON的面积.21. “十一”期间,某花店以每盆20元的价格购进一批花卉、市场调查反映:该花卉每盆售价25元时,每天可卖出25盆、若涨价销售,每盆花卉每涨价1元,每天要少卖出1盆.(1)、若该花卉每天的销售利润为200元,且销量尽可能大,每盆花卉售价是多少元?(2)、为了让利给顾客,该花店决定每盆花卉涨价不超过6元,问该花卉一天最大的销售利润是多少元?22. 如图,正方形ABCD与正方形AEFG的边长分别为和2,现在将正方形AEFG绕着点A旋转.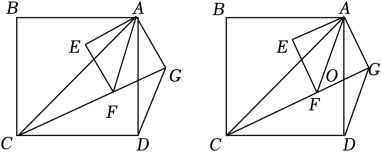 (1)、如图,连接CF、DG , 求证:△ACF∽△ADG;(2)、如图,连接CF , 当点F在△ACD内,且∠ACF=∠FAD时,设AD、FG的交点为O , 求AO的长.23. 如图,AB是⊙O的直径,弦CD⊥AB于点E , G是弧AC上一点,AG , DC的延长线交于点F , 连接AD , GD , GC .
(1)、如图,连接CF、DG , 求证:△ACF∽△ADG;(2)、如图,连接CF , 当点F在△ACD内,且∠ACF=∠FAD时,设AD、FG的交点为O , 求AO的长.23. 如图,AB是⊙O的直径,弦CD⊥AB于点E , G是弧AC上一点,AG , DC的延长线交于点F , 连接AD , GD , GC . (1)、求证:∠ADG=∠F;(2)、已知AE=CD , BE=2.
(1)、求证:∠ADG=∠F;(2)、已知AE=CD , BE=2.①求⊙O的半径长;
②若点G是AF的中点,求DF的长.
24. (1)、问题发现
(1)、问题发现如图(1),在△OAB和△OCD中,OA=OB , OC=OD , ∠AOB=∠COD=40°,连接AC、BD交于点M . 填空:
①的值为 ;②∠AMB的度数为 .
(2)、类比探究如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°, , 连接AC , 交BD的延长线于点M . 请求出的值及∠AMB的度数,并说明理由.
25. 如图,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点(点A在点B的左侧),与y轴交于点C . (1)、求抛物线的解析式;(2)、在抛物线的对称轴上存在一点P , 使得PA+PC的值最小,求此时点P的坐标;(3)、点D是第一象限内抛物线上的一个动点(不与点C、B重合),过点D作DF⊥x轴于点F , 交直线BC于点E , 连接BD , 直线BC把△BDF的面积分成两部分,若S△BDE:S△BEF=3:2,请求出点D的坐标.
(1)、求抛物线的解析式;(2)、在抛物线的对称轴上存在一点P , 使得PA+PC的值最小,求此时点P的坐标;(3)、点D是第一象限内抛物线上的一个动点(不与点C、B重合),过点D作DF⊥x轴于点F , 交直线BC于点E , 连接BD , 直线BC把△BDF的面积分成两部分,若S△BDE:S△BEF=3:2,请求出点D的坐标.