黑龙江省齐齐哈尔市铁锋区2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-01-16 类型:期末考试
一、选择题(每小题3分,满分30分)
-
1. 改革开放以来,我国众多科技实体在各自行业取得了举世瞩目的成就,大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表.上述四个企业的标志是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一个木工师傅现有两根木条,它们的长度分别为30和80,现在要做一个三角形的木架,则第三根木条应选取( )A、10 B、70 C、130 D、403. 下列各式正确的是( )A、= B、= C、= D、=4. 甲、乙两人加工一批零件,甲完成100个与乙完成80个所用的时间相同,已知甲比乙每天多完成3个.设甲每天完成个零件,依题意下面所列方程正确的是( )A、 B、 C、 D、5. 一个多边形的每一个内角都相等,且每个内角与相邻外角度数比均为 , 则这个正多边形的边数为( )A、5 B、6 C、7 D、86. 如图,四边形是一个长方形,利用不同的方法可以计算出长方形的面积.通过分析图形中所标线段的长度,将多项式因式分解,其结果正确的是( )
2. 一个木工师傅现有两根木条,它们的长度分别为30和80,现在要做一个三角形的木架,则第三根木条应选取( )A、10 B、70 C、130 D、403. 下列各式正确的是( )A、= B、= C、= D、=4. 甲、乙两人加工一批零件,甲完成100个与乙完成80个所用的时间相同,已知甲比乙每天多完成3个.设甲每天完成个零件,依题意下面所列方程正确的是( )A、 B、 C、 D、5. 一个多边形的每一个内角都相等,且每个内角与相邻外角度数比均为 , 则这个正多边形的边数为( )A、5 B、6 C、7 D、86. 如图,四边形是一个长方形,利用不同的方法可以计算出长方形的面积.通过分析图形中所标线段的长度,将多项式因式分解,其结果正确的是( )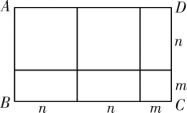 A、 B、 C、 D、7. 如图,是的中线,是上一点,交于 , 若 , 则的长度为( )
A、 B、 C、 D、7. 如图,是的中线,是上一点,交于 , 若 , 则的长度为( )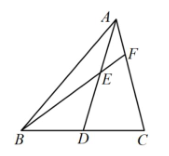 A、2.5 B、2 C、1.5 D、18. 若关于的方程无解,则的值是( )A、2 B、2或1 C、2或 D、9. 如图,已知,三角形全等于三角形 , 若 , 则的度数( )
A、2.5 B、2 C、1.5 D、18. 若关于的方程无解,则的值是( )A、2 B、2或1 C、2或 D、9. 如图,已知,三角形全等于三角形 , 若 , 则的度数( )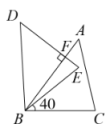 A、 B、 C、 D、10. 如图,在四边形中,平分于点 , 则面积的最大值为( )
A、 B、 C、 D、10. 如图,在四边形中,平分于点 , 则面积的最大值为( ) A、2 B、2.5 C、4 D、5
A、2 B、2.5 C、4 D、5二、填空题(每小题3分,满分21分)
-
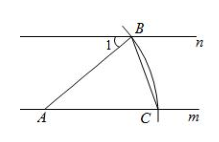
11. 某个小微粒的直径为 , 用科学记数法表示这个数为 .12. 如果分式的值为零,那么 .13. 若关于的二次三项式是完全平方式, .14. 已知 , 则 .15. 一个等腰三角形两边的长分别为3和8,那么这个等腰三角形的周长是 .16. 如图,直线 , 以直线上的点为圆心,适当长为半径画弧,分别交直线于点 , , 连接 . 若 , 则的度数为 .
 17. 在平面直角坐标系中,若干个等腰直角三角形按如图所示的规律摆放.点从原点出发,沿着“”的路线运动(每秒一条直角边),已知坐标为 , 设第秒运动到点(为正整数),则点的坐标是 .
17. 在平面直角坐标系中,若干个等腰直角三角形按如图所示的规律摆放.点从原点出发,沿着“”的路线运动(每秒一条直角边),已知坐标为 , 设第秒运动到点(为正整数),则点的坐标是 .
三、解答题(本题共7道大题,满分69分)
-
18. 计算:(1)、(2)、19. 因式分解:(1)、(2)、20. 解方程:(1)、 ;(2)、 .21. 如图,三个顶点坐标分别是
 (1)、请画出关于轴对称的;(2)、直接写出的坐标;(3)、求出的面积.22. 超市分两次购进甲、乙两种商品若干件,进货总价如下表:
(1)、请画出关于轴对称的;(2)、直接写出的坐标;(3)、求出的面积.22. 超市分两次购进甲、乙两种商品若干件,进货总价如下表:甲
乙
第一次
1500元
1200元
第二次
总共不超过1600元
(1)、第一次购进甲商品件数是乙商品件数的2倍,且甲商品的单价比乙商品的单价便宜15元/件,求甲商品的单价;(2)、第二次共购进50件,两种商品的单价与第一次相比,甲提高了 , 乙降价了 , 问此次最多购进乙商品多少件.23. 综合与实践:已知:如图,在中,厘米,厘米,点为的中点.
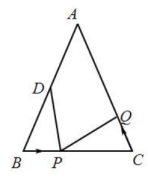 (1)、如果点在线段上以3厘米/秒的速度由点向点运动,同时,点在线段上由点向点运动,运动的时间秒.
(1)、如果点在线段上以3厘米/秒的速度由点向点运动,同时,点在线段上由点向点运动,运动的时间秒.①若点的运动速度与点的运动速度相等,时,与是否全等(填“是”或“否”);
②若点的运动速度与点的运动速度不相等,当与全等时,请直接写出点的运动速度为 ▲ .
(2)、若点以(1)①中的运动速度从点出发,点以原来的运动速度从点同时出发,都逆时针沿三边运动,则经过多长时间,点与点第一次在的哪条边上相遇?此时相遇点距离B点的路程是多少?24. 综合与实践,如图,已知 , 直线与交于点 , 与交于点 , 射线和射线交于点 . (1)、若平分平分 , 则;(2)、若 , 则;(3)、将(2)中“”改为“”,其余条件不变,求的度数(用含的代数式表示);(4)、若将分成两部分,也将分成两部分, , 则的度数(用含的代数式表示).
(1)、若平分平分 , 则;(2)、若 , 则;(3)、将(2)中“”改为“”,其余条件不变,求的度数(用含的代数式表示);(4)、若将分成两部分,也将分成两部分, , 则的度数(用含的代数式表示).