天津市五所重点高中2023-2024届高三数学联考试卷
试卷更新日期:2024-01-15 类型:高考模拟
一、单选题(本大题共9小题,共45.0分.在每小题列出的选项中,选出符合题目的一项)
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 设命题 : , ,则 的否定为( )A、 , B、 , C、 , D、 ,3. 函数的图象大致形状是( )A、
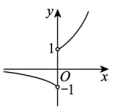 B、
B、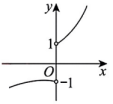 C、
C、 D、
D、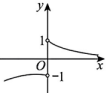 4. 直线 , 则“或”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 设a=2.10.3 , b=log43,c=log21.8,则a、b、c的大小关系为( )A、 B、 C、 D、6. 已知是等差数列的前项和,为数列的前项和,若 , 则( )A、51 B、52 C、84 D、1047. 木楔子在传统木工中运用广泛,它使得榫卯配合的牢度得到最大化满足,是一种简单的机械工具,是用于填充器物的空隙使其牢固的木橛、木片等.如图为一个木楔子的直观图,其中四边形ABCD是边长为1的正方形,且均为正三角形, , 则该木楔子的体积为( )
4. 直线 , 则“或”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 设a=2.10.3 , b=log43,c=log21.8,则a、b、c的大小关系为( )A、 B、 C、 D、6. 已知是等差数列的前项和,为数列的前项和,若 , 则( )A、51 B、52 C、84 D、1047. 木楔子在传统木工中运用广泛,它使得榫卯配合的牢度得到最大化满足,是一种简单的机械工具,是用于填充器物的空隙使其牢固的木橛、木片等.如图为一个木楔子的直观图,其中四边形ABCD是边长为1的正方形,且均为正三角形, , 则该木楔子的体积为( )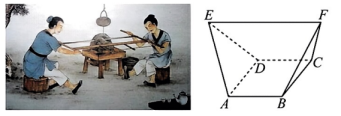 A、 B、 C、 D、8. 已知函数的部分图象如图所示,则下列说法正确的是( )
A、 B、 C、 D、8. 已知函数的部分图象如图所示,则下列说法正确的是( )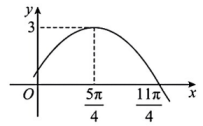 A、 B、 C、不等式的解集为 D、将的图象向右平移个单位长度后所得函数的图象在上单调递增9. 已知函数 , 若关于的方程恰有6个不同的实数根,则的取值范围是( )A、 B、 C、 D、
A、 B、 C、不等式的解集为 D、将的图象向右平移个单位长度后所得函数的图象在上单调递增9. 已知函数 , 若关于的方程恰有6个不同的实数根,则的取值范围是( )A、 B、 C、 D、二、填空题(本大题共6小题,共30.0分)
-
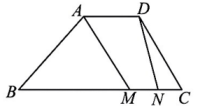
10. 已知复数 , 则复数的虚部为11. 已知圆和圆 , 则圆与圆的公共弦的弦长 .12. 曲线在处的切线的倾斜角为 , 则.13. 定义在上的函数满足 , 且时, , 则 .14. 若 , 且 , 则的最小值为;此时.15. 如图,在四边形ABCD中, , 且则实数的值为 , 若M,N是线段BC上的动点,且 , 则的最小值为.
三、解答题(本大题共5小题,共60.0分.解答应写出文字说明,证明过程或演算步骤)
-
16. 在△ABC中,角A,B,C所对的边分别为a,b,c,且 , , .(1)、求c;(2)、求的值;(3)、求的值.17. 如图,在四棱雉中,平面ABCD,底面ABCD是直角梯形,其中 , 为棱BC上的点,且.
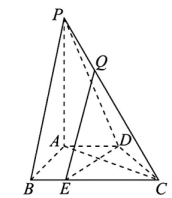 (1)、求证:平面PAC(2)、求平面APC与平面PCD所成的余弦值;(3)、设Q为棱CP上的点(不与C,p重合),且直线QE与平面PAC所成角的正弦值为 , 求的值.
(1)、求证:平面PAC(2)、求平面APC与平面PCD所成的余弦值;(3)、设Q为棱CP上的点(不与C,p重合),且直线QE与平面PAC所成角的正弦值为 , 求的值.