重庆市巴蜀名校2023-2024学年高三上学期数学适应性月考（五）试卷

试卷更新日期：2024-01-15 类型：月考试卷

进入出卷网下载

一、单项选择题(本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项是符合题目要求的)

1. 已知复数 $z = \frac{i - i^{4}}{{(1 - i)}^{2}}$ ，则 $| z | =$ （）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{1}{2}$ C、 $\sqrt{2}$ D、 $\frac{3}{2}$

查看试题解析
2. 已知集合 $A = {x | l o g_{2}^{2} x - 3 l o g_{2} x < 0}$ ， $B = {y | y = 3 x - 1 ， x \in N}$ ，则 $A ∩ B =$ （）

A、 ${2 ， 5 ， 8}$ B、 ${- 1 ， 2 ， 5}$ C、 ${5 ， 8}$ D、 ${2 ， 5}$

查看试题解析
3. 古希腊数学家欧几里得在《几何原本》里提出：“球的体积（V）与它的直径（D）的立方成正比”，即 $V = k D ³$ ，但欧几里得未给出常数k的值. 现算出 k 的值，进而可得 $c o s k =$ （）

A、0 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
4. 定义域为R的函数 $f (x)$ 关于 $x = 1$ 对称，且当 $x_{2} > x_{1} > 1$ 时， $\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} > 0$ 恒成立，设 $a = f (s i n \frac{π}{3}) ， b = f (\frac{2}{3}) ， c = f (2) ，$ 则（）

A、 $c > a > b$ B、 $c > b > a$ C、 $a > c > b$ D、 $b > c > a$

查看试题解析
5. 已知直线 $l_{1}$ 过点 $A (0 ， 1)$ ，直线 $l_{1}$ 与直线 $l_{2} ： y = x$ 的交点B在第一象限，点O为坐标原点. 若三角形OAB为钝角三角形时，则直线 $l_{1}$ 的斜率的范围是（）

A、 $(- \infty ， - 1]$ B、 $(- \infty ， - 1) \cup (0 ， + \infty)$ C、 $(- \infty ， - 1) \cup (0 ， 1)$ D、 $(- \infty ， - 1) \cup (1 ， + \infty)$

查看试题解析
6. 在三棱锥 $P - A B C$ 中， $P A = \sqrt{5}$ ， $P A ⊥$ 平面 $A B C$ ， D为BC 的中点且 $P D = 2 \sqrt{2} ，$ 当 $△ A B C$ 为正三角形时，三棱锥 $P - A B C$ 外接球的表面积为（）

A、 $10 π$ B、 $\frac{31 π}{3}$ C、 $4 π$ D、 $\frac{31 π}{12}$

查看试题解析
7. 若关于 x 的方程 $2 s i n x c o s x - \sqrt{3} c o s 2 x = 1$ 在 $[0 ， π)$ 内有两个不同的解 $x_{1}$ ， $x_{2}$ ，则 $s i n (x_{1} + x_{2})$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{2} + \sqrt{6}}{4}$

查看试题解析
8. 已知数列 ${a_{n}}$ 的前 n 项和 $S_{n} = 2 a_{n} - 2^{n + 1}$ ，不等式 $(m ² - 10 m) a_{n} \leq (n - 19) S_{n}$ 对任意 $n \in N *$ 恒成立，则实数m的最大值为（）

A、4 B、6 C、8 D、2

查看试题解析

二、多项选择题(本大题共4个小题，每小题5分，共20分，在每个给出的四个选项中，有多项是满足要求的，全部选对的得5分，部分选对的得2分，有选错的得0分)

9. 小明参加唱歌比赛，现场8位评委给分分别为： 15， 16， 18， 20， 20， 22， 24， 25.按比赛规则，计算选手最后得分成绩时，要先去掉评委给分中的最高分和最低分. 现去掉这组得分中的最高分和最低分后，下列数字特征的值不会发生变化的是（）

A、平均数 B、极差 C、中位数 D、众数

查看试题解析
10. 设抛物线C： $y ² = 2 p x$ 的焦点为F ，准线为 $x = - 1$ . 点A ， B是抛物线C上不同的两点，且 $| A F | + | B F | = 8$ ，则（）

A、 $p = 2$ B、以线段 $A B$ 为直径的圆必与准线相切 C、线段 $A B$ 的长为定值 D、线段 $A B$ 的中点 E 到准线的距离为定值

查看试题解析
11. 已知向量 $\vec{a} ， \vec{b} ， \vec{c}$ 满足 $| \vec{a} | = 3 ， | \vec{b} | = 1 ， | 2 \vec{a} - \vec{b} | = \sqrt{31} ， | \vec{c} | = 2 | \vec{c} - \vec{a} |$ ，设 $\vec{m} = t \vec{b}$ $(t \in R)$ ，则（）

A、 $\vec{a} \cdot \vec{b} = 2$ B、 $\vec{a} + \vec{b}$ 在 $\vec{b}$ 方向上的投影向量为 $\frac{5}{2} \vec{b}$ C、 $| \vec{m} - \vec{c} |$ 的最小值为 $2 \sqrt{3} - 2$ D、 $| \vec{m} - \vec{c} |$ 无最大值

查看试题解析
12. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为 $2$ ， $O$ 是空间中的一动点，下列结论正确的是（）

A、若点 $O$ 在正方形 $D C C_{1} D_{1}$ 内部，异面直线 $A_{1} B_{1}$ 与OB所成角为θ ，则θ的取值范围为 $(\frac{π}{4} ， \frac{π}{2})$ B、若点 $O$ 在正方形 $D C C_{1} D_{1}$ 内部，且 $| O B | = \sqrt{5} ，$ 则点 $O$ 的轨迹长度为 $\frac{1}{4} π$ C、若 $\vec{A O} = \frac{1}{4} \vec{A B} + λ \vec{A D} (0 \leq λ \leq 1)$ ，则 $B_{1} O + O D$ 的最小值为 $\sqrt{13}$ D、若 $\vec{A O} = λ \vec{A B} + (1 - λ) \vec{A D} (0 \leq λ \leq 1)$ ，平面 $O A D_{1}$ 截正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 所得截面面积的最大值为 $3 \sqrt{3}$

查看试题解析

三、填空题(本大题共4小题，每小题5分，共20分)

13. 已知两个等差数列 ${a_{n}}$ ， ${b_{n}}$ 的前n项和分别为 $S_{n}$ ， $T_{n}$ . 若 $\frac{a_{5}}{b_{5}} = 2 ，$ 则 $\frac{S_{9}}{T_{9}} =$ .

查看试题解析
14. 在三棱台 $A B C - A_{1} B_{1} C_{1}$ 中，已知 $A C = B C = 2 ， A_{1} C_{1} = B_{1} C_{1} = 1 ， A C ⊥ B C ， C C_{1} ⊥$ 平面 $A B C$ ， $∠ A_{1} A C = 6 0^{∘}$ ，则该三棱台的体积为.

查看试题解析
15. 已知动点 $M (x ， y)$ 满足 ${\begin{array}{l} x = 2 + 2 c o s θ \\ y = 2 s i n θ \end{array} (θ \in R)$ ，若直线l过点 $(- 2 ， 0)$ 与点M的轨迹相切，则直线l的方程为.

查看试题解析
16. 若不等式 $e^{\frac{x}{2}} (2 m l n x - x + 1) \leq x^{m} （ m > 0 ）$ 对任意的 $x \in (0 ， + \infty)$ 恒成立，则实数m的最大值为.

查看试题解析

四、解答题(共70分，解答应写出文字说明，证明过程或演算步骤)

17. 已知 $△ A B C$ 的内角A ， B ， C所对应的边分别为a ， b ， c ，且满足 $\frac{a}{b + c} + \frac{b s i n B}{b s i n A + c s i n B} = 1 .$

(1)、求角C的大小；

(2)、若 $a = 2 ， b = 4$ ，点D为AB 的中点，求 $t a n ∠ A C D$ 的值.

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中，四边形ABCD是直角梯形， $P C ⊥$ 平面ABCD ， $A D ⊥ A B$ ， $A B$ ∥ $D C$ ， $A B = 2 A D = 2 C D$ ，点 E 是 PB 的中点.

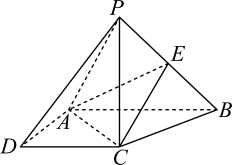(1)、证明：平面 $P A C ⊥$ 平面 PBC；

(2)、若平面 PAD 与平面 ABCD 所成锐二面角的正切值为2，求直线PD 与平面ACE 所成角的正弦值.

查看试题解析
19. 已知递增等比数列 ${a_{n}}$ 中， $a_{1} = 2$ ， $2 a_{1} ， \frac{3}{2} a_{2} ， a_{3}$ 成等差数列.

(1)、求数列 ${l o g_{2} a_{n}}$ 的前n项和 $S_{n}$ ；

(2)、若 $b_{n} = a_{n} \cdot l o g_{2} a_{n}$ 设数列 ${b_{n}}$ 的前n项和为 $T_{n}$ ，求使得 $T_{n} \geq 2024$ 的最小正整数n的值.

查看试题解析
20. 已知函数 $f (x) = l n x + 1 ， g (x) = a x^{2} (a > 0) .$

(1)、当 $a = 2$ 时，求 $y = f (x) - g (x)$ 的极值；

(2)、若曲线 $y = f (x)$ 与曲线 $y = g (x)$ 存在2 条公切线，求a的取值范围.

查看试题解析
21. 重庆南山风景秀丽，可以俯瞰渝中半岛，是徒步休闲的好去处. 上南山的步道很多，目前有标识的步道共有 18条. 某徒步爱好者俱乐部发起一项活动，若挑战者连续12天每天完成一次徒步上南山(每天多次上山按一次计算) 运动，即可获得活动大礼包. 已知挑战者甲从11月1号起连续12天都徒步上南山一次，每次只在凉水井步道和清水溪步道中选一条上山. 甲第一次选凉水井步道上山的概率为 $\frac{3}{4} ，$ 而前一次选择了凉水井步道，后一次继续选择凉水井步道的概率为 $\frac{1}{4} ，$ 前一次选择清水溪步道，后一次继续选择清水溪步道的概率为 $\frac{1}{2}$ ，如此往复. 设甲第n(n=1，2，…， 12)天走凉水井步道上山的概率为 $P_{n}$ .

(1)、求 $P_{2}$ 和 $P_{n}$ ；

(2)、求甲在这12 天中选择走凉水井步道上山的概率小于选择清水溪步道上山概率的天数.

查看试题解析
22. 已知点 $P (x_{0} ， y_{0})$ 是椭圆E： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 上的动点，离心率 $e = \frac{\sqrt{3}}{2} ，$ 设椭圆左、右焦点分别为 $F_{1} ， F_{2}$ ，且 $| P F_{1} | + | P F_{2} | = 4$

(1)、求椭圆E的标准方程；

(2)、若直线 $P F_{1} ， P F_{2}$ 与椭圆C的另一个交点分别为A ， B ，问 $△ P A B$ 面积是否存在最大值，若存在，求出最大值；若不存在，请说明理由.

查看试题解析

重庆市巴蜀名校2023-2024学年高三上学期数学适应性月考（五）试卷

一、单项选择题(本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项是符合题目要求的)

二、多项选择题(本大题共4个小题， 每小题5分，共20分，在每个给出的四个选项中，有多项是满足要求的，全部选对的得5分，部分选对的得2分，有选错的得0分)

三、填空题(本大题共4小题，每小题5分，共20分)

四、解答题(共70分，解答应写出文字说明，证明过程或演算步骤)

二、多项选择题(本大题共4个小题，每小题5分，共20分，在每个给出的四个选项中，有多项是满足要求的，全部选对的得5分，部分选对的得2分，有选错的得0分)