重庆市黔江区重点中学校2023-2024学年高二上学期数学12月月考试卷
试卷更新日期:2024-01-15 类型:月考试卷
一、单选题(本大题共8小题,共40分。在每小题列出的选项中,选出符合题目的一项)
-
1. 在平面直角坐标系中,直线:的倾斜角为( )A、 B、 C、 D、2. 已知双曲线的一条渐近线方程为 , 则( )A、 B、 C、 D、3. 用火柴棒“
 ”摆“金鱼”,如下图所示:
”摆“金鱼”,如下图所示: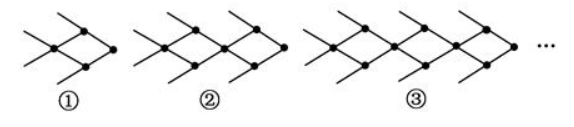
按照上面的规律,第个“金鱼”图形需要火柴棒的根数为( )
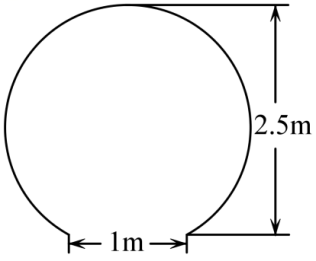
A、 B、 C、 D、4. “圆”是中国文化的一个重要精神元素,在中式建筑中有着广泛的运用,最具代表性的便是园林中的门洞.如图,某园林中的圆弧形门洞高为 , 底面宽为 , 则该门洞的半径为( )
 A、 B、 C、 D、5. 已知等差数列an中,a2+a4=6,则a1+a2+a3+a4+a5=( )A、30 B、15 C、 D、6. 已知是双曲线的两个焦点,为上一点,且 , 则的离心率为( )A、 B、 C、 D、7. 在我国古代数学名著九章算术中,将底面为直角三角形,且侧棱垂直于底面的棱柱称为堑堵.已知在堑堵中, , , , 若直线与直线所成角为 , 则( )
A、 B、 C、 D、5. 已知等差数列an中,a2+a4=6,则a1+a2+a3+a4+a5=( )A、30 B、15 C、 D、6. 已知是双曲线的两个焦点,为上一点,且 , 则的离心率为( )A、 B、 C、 D、7. 在我国古代数学名著九章算术中,将底面为直角三角形,且侧棱垂直于底面的棱柱称为堑堵.已知在堑堵中, , , , 若直线与直线所成角为 , 则( )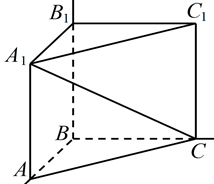 A、 B、 C、 D、8. 如图,已知抛物线:和圆: , 过抛物线的焦点作直线与上述两曲线自左而右依次交于点 , , , , 则的最小值为( )
A、 B、 C、 D、8. 如图,已知抛物线:和圆: , 过抛物线的焦点作直线与上述两曲线自左而右依次交于点 , , , , 则的最小值为( )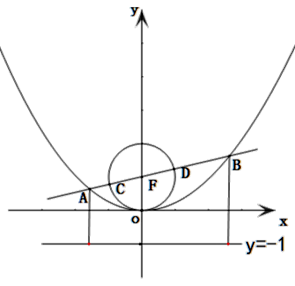 A、 B、 C、 D、
A、 B、 C、 D、二、多选题(本大题共4小题,共20分。在每小题有多项符合题目要求)
-
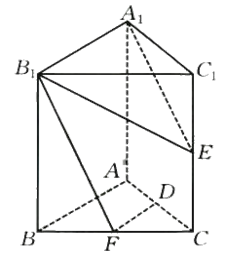
9. 已知直线 , 直线 , 则( )A、当时,与的交点为 B、直线恒过点 C、若 , 则 D、存在 , 使10. 已知圆和圆的交点为 , , 则( )A、两圆的圆心距 B、直线的方程为 C、圆上存在两点和使得 D、圆上的点到直线的最大距离为11. “奔跑吧少年”青少年阳光体育系列赛事活动于近日开赛,本次比赛的总冠军奖杯由一个铜球和一个托盘组成,如图 , 已知球的体积 , 托盘由边长为的正三角形钢片沿各边中点的连线垂直向上折叠而成,(即面ADE,面CDF,面BEF均垂直于底面DEF),如图 , 则下列结论正确的是( )
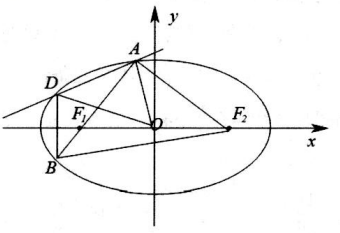
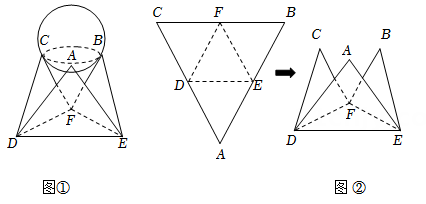 A、直线与平面所成的角为 B、直线平面 C、异面直线与所成的角的余弦值为 D、球上的点离球托底面的最大距离为12. 已知点为双曲线上任意一点,、为其左、右焦点,为坐标原点.过点向双曲线两渐近线作垂线,设垂足分别为、 , 则下列所述正确的是( )A、为定值 B、、、、四点一定共圆 C、的最小值为 D、存在点满足、、三点共线时,、、三点也共线
A、直线与平面所成的角为 B、直线平面 C、异面直线与所成的角的余弦值为 D、球上的点离球托底面的最大距离为12. 已知点为双曲线上任意一点,、为其左、右焦点,为坐标原点.过点向双曲线两渐近线作垂线,设垂足分别为、 , 则下列所述正确的是( )A、为定值 B、、、、四点一定共圆 C、的最小值为 D、存在点满足、、三点共线时,、、三点也共线三、填空题(本大题共4小题,共20分)
-
13. 经过A(0,2),B(-1,0)两点的直线的方向向量为(1,k),则k=.14. 已知数列 , , , , , , , , , , , , 则该数列的第项为.15. 过点P作圆切线,记切点分别为A,B,则 .16. 斐波那契数列因意大利数学家斐波那契以兔子繁殖为例引入,故又称为“兔子数列”,即 , , , , , , , , , , , , , 在实际生活中,很多花朵如梅花、飞燕草、万寿菊等的瓣数恰是斐波那契数列中的数,斐波那契数列在现代物理及化学等领域也有着广泛的应用.斐波那契数列满足: , , 经计算发现:(),则m= .
四、解答题(本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤)
-
17. 已知等差数列 , , 其中仍成等差数列.(1)、求数列的通项公式;(2)、求数列的前项和 , 且 , 求 .18. 已知圆C的圆心为C,且过点 , .(1)、当AB为直径时,圆C的面积取得最小值,求此时圆C的标准方程及圆C的面积;(2)、对于中的圆,设过点的直线与圆C所截得弦长为2 , 求直线的方程.19. 如图,四棱锥的底面是边长为的正方形,侧面底面 , 且分别为棱的中点.
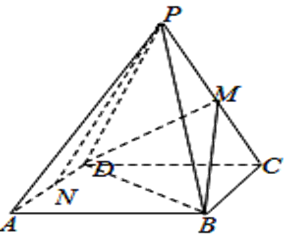 (1)、求证:;(2)、求点到平面的距离.20. 已知是抛物线(>0)的焦点,抛物线上点A满足AF垂直于x轴,且 .(1)、求抛物线C的标准方程;(2)、、是该抛物线上的两点, , 求线段的中点到轴的距离;(3)、已知点H(1,1),直线过点与抛物线交于 , 两个不同的点均与点H不重合 , 设直线 , 的斜率分别为 , , 求证:为定值.
(1)、求证:;(2)、求点到平面的距离.20. 已知是抛物线(>0)的焦点,抛物线上点A满足AF垂直于x轴,且 .(1)、求抛物线C的标准方程;(2)、、是该抛物线上的两点, , 求线段的中点到轴的距离;(3)、已知点H(1,1),直线过点与抛物线交于 , 两个不同的点均与点H不重合 , 设直线 , 的斜率分别为 , , 求证:为定值.