安徽省宿州市萧县2023-2024学年八年级上学期期中数学试卷
试卷更新日期:2024-01-15 类型:期中考试
一、选择题(本大题共10小题,每小题4分,共40分)
-
1. 如图,在△ABC中, , , 以AB,AC为边作正方形,这两个正方形的面积和为( )
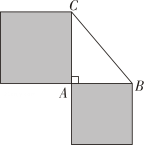 A、6 B、36 C、16 D、492. 最简二次根式 与 是能够合并的二次根式,则x的值为( )A、1 B、﹣2 C、﹣1 D、03. 如图,在正方形OABC中,O是坐标原点,点A的坐标为(1,),则点C的坐标是( )
A、6 B、36 C、16 D、492. 最简二次根式 与 是能够合并的二次根式,则x的值为( )A、1 B、﹣2 C、﹣1 D、03. 如图,在正方形OABC中,O是坐标原点,点A的坐标为(1,),则点C的坐标是( ) A、(﹣ , 1) B、(﹣1,) C、(﹣ , 1) D、(﹣ , ﹣1)4. 甲、乙、丙、丁四个人步行的路程和所用的时间如图所示,按平均速度计算.走得最快的是( )
A、(﹣ , 1) B、(﹣1,) C、(﹣ , 1) D、(﹣ , ﹣1)4. 甲、乙、丙、丁四个人步行的路程和所用的时间如图所示,按平均速度计算.走得最快的是( )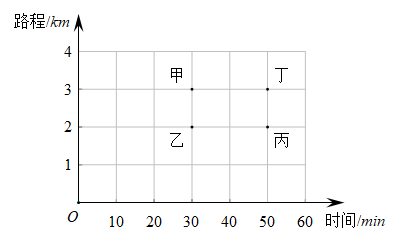 A、甲 B、乙 C、丙 D、丁5. 小李、小王、小张、小谢原有位置如图,若用表示小李的位置,表示小王的位置,表示小张的位置,表示小谢的位置.撤走最上面一行,仍按照原有确定位置的方法确定新的位置,下列说法正确的是( )
A、甲 B、乙 C、丙 D、丁5. 小李、小王、小张、小谢原有位置如图,若用表示小李的位置,表示小王的位置,表示小张的位置,表示小谢的位置.撤走最上面一行,仍按照原有确定位置的方法确定新的位置,下列说法正确的是( ) A、小李现在位置为 B、小张现在位置为 C、小王现在位置为 D、小谢现在位置为6. 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图);如果大正方形的面积是 , 小正方形的面积是 , 直角三角形的两直角边分别为、 , 那么的值是( )
A、小李现在位置为 B、小张现在位置为 C、小王现在位置为 D、小谢现在位置为6. 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图);如果大正方形的面积是 , 小正方形的面积是 , 直角三角形的两直角边分别为、 , 那么的值是( )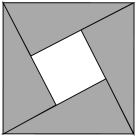 A、 B、 C、 D、7. 如图,一次函数y1=x与y2=kx+b的图象相交于点P,则函数y=(k﹣1)x+b的图象可能是( )
A、 B、 C、 D、7. 如图,一次函数y1=x与y2=kx+b的图象相交于点P,则函数y=(k﹣1)x+b的图象可能是( ) A、
A、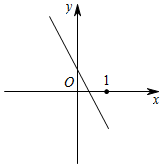 B、
B、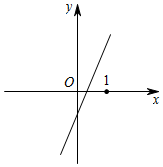 C、
C、 D、
D、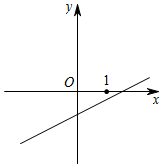 8. 在平面直角坐标系中,点A(﹣1,1)在直线 y=x+b上,过点A作A1B1⊥x轴于点B1 , 作等腰直角三角形A1B1B2(B2与原点O重合),再以A1B2为腰作等腰直角三角形A2A1B2 , 以 A2B2为腰作等腰直角三角形A2B2B3…按照此规律进行下去,那么A2020的坐标为( )
8. 在平面直角坐标系中,点A(﹣1,1)在直线 y=x+b上,过点A作A1B1⊥x轴于点B1 , 作等腰直角三角形A1B1B2(B2与原点O重合),再以A1B2为腰作等腰直角三角形A2A1B2 , 以 A2B2为腰作等腰直角三角形A2B2B3…按照此规律进行下去,那么A2020的坐标为( ) A、(22019﹣1,22019) B、(22020﹣2,22020) C、(22020﹣1,22020) D、(22019﹣2,22019)
A、(22019﹣1,22019) B、(22020﹣2,22020) C、(22020﹣1,22020) D、(22019﹣2,22019)二、填空题(本大题共4小题,每小题5分,满分20分)
-
9. 的平方根是;的算术平方根是 .10. 某物体在力F的作用下,沿力的方向移动的距离为s,力对物体所做的功W与s的对应关系如图所示,则W与s之间的关系式是: .
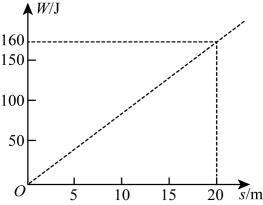 11. 如图是一个数值转换器,当输入x的值为324时,则输出y的值是 .
11. 如图是一个数值转换器,当输入x的值为324时,则输出y的值是 .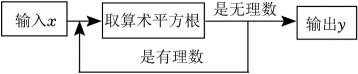 12. 如图在平面直角坐标系中,A、B两点坐标分别为A(2,﹣3),B(4,﹣1).
12. 如图在平面直角坐标系中,A、B两点坐标分别为A(2,﹣3),B(4,﹣1).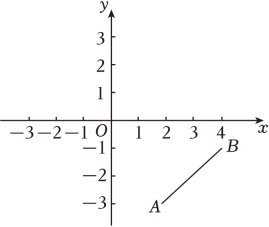 (1)、若点C是x轴上一个动点,当△ABC的周长最短时,最短周长是 .(2)、设M、N分别为x轴和y轴上的动点,存在这样的点M、N,使四边形ABMN的周长最短,最短周长是 .
(1)、若点C是x轴上一个动点,当△ABC的周长最短时,最短周长是 .(2)、设M、N分别为x轴和y轴上的动点,存在这样的点M、N,使四边形ABMN的周长最短,最短周长是 .三、解答题(本大题共4题,每题8分,满分32分)
-
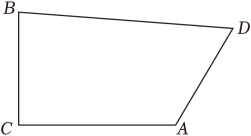
13.(1)、;(2)、求x的值:4(x+1)2﹣9=0.14. 在平面直角坐标系中,已知点M(2﹣m,1+2m).(1)、若点M到y轴的距离是2,求M点的坐标;(2)、若点M在第一、三象限的角平分线上,直线 y=kx+b 经过点M和(0,5)两点,求该直线的表达式.15. 学校正在增加绿化区域,种植花草树木,提高校园的绿化覆盖率,准备在四边形的空地上种植花卉,如图所示, , , , , , 求四边形的面积.
 16. 已知2a+5的平方根是±3,2b﹣a的立方根是2,c是的整数部分.(1)、求a、b、c的值;(2)、求a+2b﹣c的算术平方根.
16. 已知2a+5的平方根是±3,2b﹣a的立方根是2,c是的整数部分.(1)、求a、b、c的值;(2)、求a+2b﹣c的算术平方根.四、(本大题共2题,每小题10分,满分20分)
-
17. 已知,点A(0,1),B(2,0),C(4,3).
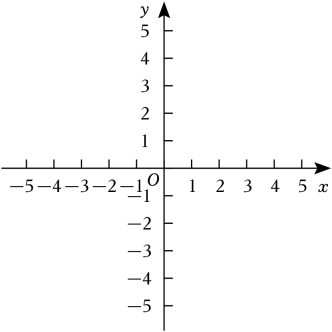
⑴在坐标系中画出△ABC;
⑵求△ABC的面积;
⑶画出△ABC关于x轴的对称图形△A1B1C1 , 并写出点A1 , B1 , C1的坐标.
18. 定义新运算:a⊗b=a(1﹣b),其中等号右边是常规的乘法和减法运算,例如:(﹣1)⊗1=(﹣1)×(1﹣1)=0.(1)、计算:(1+ )⊗ ;(2)、嘉淇说:若a+b=0,则a⊗a+b⊗b=2ab , 你是否同意他的观点,请说明理由.五、(本大题共2题,每小题12分,满分24分)
-
19. 拉杆箱是人们出行的常用品,采用拉杆箱可以让人们出行更轻松.如图,已知某种拉杆箱箱体长AB=65cm,拉杆最大伸长距离BC=35cm,在箱体底端装有一圆形滚轮,当拉杆拉到最长时,滚轮的圆心在图中的A处,点A到地面的距离AD=3cm,当拉杆全部缩进箱体时,滚轮圆心水平向右平移55cm到A′处,求拉杆把手C离地面的距离(假设C点的位置保持不变).
 20. 完善下面表格,发现平方根和立方根的规律,并运用规律解决问题.
20. 完善下面表格,发现平方根和立方根的规律,并运用规律解决问题.x
…
0.064
0.64
64
6400
64000
…
…
0.25298
0.8
8
m
252.98
…
…
n
0.8618
4
18.566
40
…
(1)、表格中的m= , n= .(2)、从表格数字中可以发现:开算术平方根时,被开方数的小数点每向左(或向右)移动两位,它的算术平方根的小数点随即向左(或向右)移动一位.请用文字表述立方根的变化规律: .(3)、若 , 求a+b的值.(参考数据:)六、(本大题共1题,满分14分)
-
21. 在平面直角坐标系中,点O为坐标原点,点A的横坐标为a,点A的纵坐标为b,且实数a,b满足 .
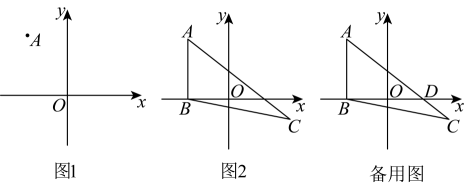 (1)、如图1,求点A的坐标;(2)、如图2,过点A作x轴的垂线,点B为垂足.若将点A向右平移10个单位长度,再向下平移8个单位长度可以得到对应点C,连接 , , 请直接写出点B,C的坐标并求出三角形的面积.(3)、在(2)的条件下,记与x轴交点为点D,点P在y轴上,连接 , , 若三角形的面积与三角形的面积相等,直接写出点P的坐标.
(1)、如图1,求点A的坐标;(2)、如图2,过点A作x轴的垂线,点B为垂足.若将点A向右平移10个单位长度,再向下平移8个单位长度可以得到对应点C,连接 , , 请直接写出点B,C的坐标并求出三角形的面积.(3)、在(2)的条件下,记与x轴交点为点D,点P在y轴上,连接 , , 若三角形的面积与三角形的面积相等,直接写出点P的坐标.