安徽省芜湖市2023-2024学年七年级上学期期中数学试卷

试卷更新日期：2024-01-15 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每题4分，共计40分）

1. 下列四个数中，最小的数是（　　）

A、﹣3 B、0 C、﹣（﹣1） D、（﹣1）²

查看试题解析
2. 下列说法中，正确的是（　　）

A、 $\frac{1}{3}$ πx²的系数是 $\frac{1}{3}$ B、 $\frac{1}{2}$ xy²的系数是 $\frac{1}{2}$ x C、3²x²的系数是3² D、﹣5x²的系数为5

查看试题解析
3. 下列计算正确的是（）

A、5a+2b=7ab B、5a³﹣3a²=2a C、4a²b﹣3ba²=a²b D、﹣ $\frac{1}{2}$ y²﹣ $\frac{1}{4}$ y²=﹣ $\frac{3}{4}$ y⁴

查看试题解析
4. 下列运算结果等于1的是（　　）

A、﹣3+（﹣3） B、﹣3﹣（﹣3） C、﹣3÷（﹣3） D、﹣3×（﹣3）

查看试题解析
5. 在﹣（﹣2），﹣|﹣7|，﹣|+1|，|﹣ $\frac{2}{3}$ |，﹣（+0.8）中负数的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 某地居民生活用水收费标准：每月用水量不超过20立方米，每立方米a元；超过部分每立方米（a+3）元．该地区某家庭上月用水量为25立方米，则应缴水费（　　）

A、25a元 B、（25a+10）元 C、（25a+15）元 D、（20a+15）元

查看试题解析
7. 观察如图，它的计算过程可以解释____这一运算规律，（）

A、加法交换律 B、乘法结合律 C、乘法交换律 D、乘法分配律

查看试题解析
8. 小嵩利用计算机设计了一个计算程序，输入和输出的数据如表：
输入
⋯
1
2
3
4
5
⋯
输出
⋯
$\frac{2}{2}$
$\frac{4}{5}$
$\frac{6}{10}$
$\frac{8}{17}$
$\frac{10}{26}$
⋯
那么，当输入数据是8时，输出的数据是（）

A、 $\frac{16}{61}$ B、 $\frac{16}{63}$ C、 $\frac{16}{65}$ D、 $\frac{16}{67}$

查看试题解析
9. 下列表格中的四个数都是按照规律填写的，则表中x的值是（　　）

A、139 B、209 C、109 D、259

查看试题解析
10. 某种型号的变速自行车的主动轴上有三个齿轮，齿数分别是48，36，24；后轴上有四个齿轮，齿数分别是32，24，16，8．则这种变速车共有（　　）档不同的车速．

A、9 B、8 C、12 D、16

查看试题解析

二、填空题（共4小题，每题5分，共计20分）

11. $- 3 \frac{1}{2}$ 的倒数是．

查看试题解析
12. 在数轴上点A表示的数是﹣1，则同一数轴上与A点相距6个单位长度的点表示的数是．

查看试题解析
13. “十一”黄金周期间，某市外出旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）
日期
1日
2日
3日
4日
5日
6日
7日
人数变化单位：万人
+1.6
+0.8
+0.4
﹣0.4
﹣0.8
+0.2
﹣1.2
如果将9月30日外出旅游人数记为a，请用含字母a的代数式表示“十一”黄金周期间该市外出旅游的总人数：．

查看试题解析
14. 如表，有12个方格，每个方格内都有一个数，若任何相邻三个数的和都是19，则x的值是．
5
A
B
C
D
E
F
x
G
H
P
10

查看试题解析

三、解答题（共9小题，共计90分）

15. 计算：

(1)、﹣12+（﹣6）﹣（﹣28）；

(2)、 $- 3^{2} + (\frac{7}{8} - 1) \times (- 2)^{2}$ ．

查看试题解析
16. 先化简，再求值：2（4a²﹣a）﹣（3a²﹣2a+5），其中，a＝﹣3．

查看试题解析
17. 某班抽查了10名同学的单元测试成绩，以85分为基准，超出的记为正数，不足的记为负数，记录的结果如下：
+8，﹣3，+12，﹣7，﹣10，﹣4，﹣8，+1，0，+10．

(1)、这10名同学中的最高分是多少？最低分是多少？

(2)、10名同学的平均成绩是多少？

查看试题解析
18. 某教辅书中一道整式运算的题参考答案部分印刷不清，形式如下：
解：原式＝+2（a²﹣2ab）＝12a²﹣5ab．

(1)、求印刷不清部分代表的整式；

(2)、当a＝﹣2，b＝3时，求印刷不清部分的值．

查看试题解析
19. 我国“华为“公司是世界通讯领域的龙头企业，某款手机后置摄像头模组如图所示，其中大圆的半径为r，中间小圆的半径为 $\frac{1}{2} r$ ， 4个半径为 $\frac{1}{5} r$ 的高清圆形镜头分布在两圆之间.

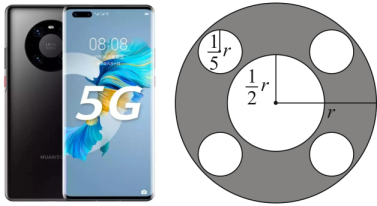(1)、请用含r的式子表示图中阴影部分的面积；

(2)、当 $r = 2$ cm时，求图中阴影部分的面积（ $π$ 取3）.

查看试题解析
20. 有理数a、b、c在数轴上的位置如图，

(1)、判断正负，用“＞”或“＜”填空：c﹣b0，a+b0，a﹣c0．

(2)、化简：|c﹣b|+|a+b|﹣2|a﹣c|．

查看试题解析
21. 如图，点A，O，B在数轴上表示的数分别为﹣6，0，10，点C是数轴上一动点，其表示的数为x．

(1)、若点C到A、B两点的距离相等，点C表示的数是；

(2)、若点C到点B的距离是点C到点A距离的3倍，则点C对应的数应是多少？请写出你的推理计算过程．

查看试题解析
22. 探索规律，观察下面等式，解答问题．
1＝1²；
1+3＝4＝2²；
1+3+5＝9＝3²；
1+3+5+7＝16＝4²；
1+3+5+7+9＝25＝5²；
…

(1)、请猜想1+3+5+7+9+…+21＝；

(2)、请猜想1+3+5+7+9+…+（2n﹣1）＝；（n是整数且n≥1）

(3)、计算：201+203+…+297+299．

查看试题解析
23. 小东对有理数a，b定义了一种新的运算，叫做“乘减法”，记作“a⊗b”．他写出了一些按照“乘减法”运算的算式：
（+3）⊗（+2）＝+1，（+11）⊗（﹣3）＝﹣8，（﹣2）⊗（+5）＝﹣3，（﹣6）⊗（﹣1）＝+5，（ $+ \frac{1}{3}$ ）⊗（+1）＝ $+ \frac{2}{3}$ ，（﹣4）⊗（+0.5）＝﹣3.5，（﹣8）⊗（﹣8）＝0，（+2.4）⊗（﹣2.4）＝0，（+23）⊗0＝+23，0⊗（﹣ $\frac{7}{4}$ ）＝+ $\frac{7}{4}$ ．
小玲看了这些算式后说：“我明白你定义的‘乘减法’法则了．”她将法则整理出来给小东看，小东说：“你的理解完全正确．”

(1)、请将下面小玲整理的“乘减法”法则补充完整：
绝对值不相等的两数相“乘减”，同号得，异号得，并；绝对值相等的两数相“乘减”，都得0；一个数与0相“乘减”，或0与一个数相“乘减”，都得这个数的绝对值．

(2)、若括号的作用与它在有理数运算中的作用相同，
①用“乘减法”计算：[（+3）⊗（﹣2）]⊗[（﹣9）⊗0]＝ ▲ ；
②小东发现交换律在有理数的“乘减法”中仍然成立，即a⊗b＝b⊗a．但是结合律在有理数的“乘减法”中不一定成立，请你举一个例子说明（a⊗b）⊗c＝a⊗（b⊗c）不成立．

查看试题解析

输入	⋯	1	2	3	4	5	⋯
输出	⋯	$\frac{2}{2}$	$\frac{4}{5}$	$\frac{6}{10}$	$\frac{8}{17}$	$\frac{10}{26}$	⋯

日期	1日	2日	3日	4日	5日	6日	7日
人数变化单位：万人	+1.6	+0.8	+0.4	﹣0.4	﹣0.8	+0.2	﹣1.2