四川省德阳市中江县2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2024-01-15 类型:期中考试
一、选择题(本大题共12个小题,每小题4分,满分48分)在每小题给出的四个选项中,有且仅有一项是符合题目要求的.
-
1. 搭载神舟十六号载人飞船的长征二号遥十六运载火箭于年月日成功发射升空,景海鹏、朱杨柱、桂海潮名航天员开启“太空出差”之旅,展现了中国航天科技的新高度.下列图标中,其文字上方的图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知二次函数y=﹣2(x﹣1)2﹣3,下列说法正确的是( )A、对称轴为直线x=﹣1 B、函数的最大值是3 C、抛物线开口向上 D、顶点坐标为(1,﹣3)3. 如图,将△ABC绕点A逆时针旋转110°,得到△ADE , 若点D落在线段BC的延长线上,则∠B大小为( )
2. 已知二次函数y=﹣2(x﹣1)2﹣3,下列说法正确的是( )A、对称轴为直线x=﹣1 B、函数的最大值是3 C、抛物线开口向上 D、顶点坐标为(1,﹣3)3. 如图,将△ABC绕点A逆时针旋转110°,得到△ADE , 若点D落在线段BC的延长线上,则∠B大小为( )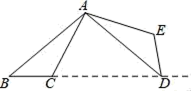 A、30° B、35° C、40° D、45°4. 甲公司前年缴税a万元,去年和今年缴税的年平均增长率均为b , 则今年该公司应缴税( )万元.A、a(1+b%)2 B、a(1+b)2 C、a(1﹣b)2 D、a(1﹣b%)25. 在平面直角坐标系中,点(2,1)关于原点对称的点的坐标是( )A、(﹣2,1) B、(2,﹣1) C、(1,2) D、(﹣2,﹣1)6. 已知m,n是方程x2+2x﹣5=0的两个实数根,则m2﹣mn+3m+n=( )A、6 B、7 C、8 D、97. 如图,已知二次函数y1=的图象与正比例函数y2=kx(k≠0)的图象相交于点A(3,4),与x轴交于点B(2,0),若0<y1<y2 , 则x的取值范围是( )
A、30° B、35° C、40° D、45°4. 甲公司前年缴税a万元,去年和今年缴税的年平均增长率均为b , 则今年该公司应缴税( )万元.A、a(1+b%)2 B、a(1+b)2 C、a(1﹣b)2 D、a(1﹣b%)25. 在平面直角坐标系中,点(2,1)关于原点对称的点的坐标是( )A、(﹣2,1) B、(2,﹣1) C、(1,2) D、(﹣2,﹣1)6. 已知m,n是方程x2+2x﹣5=0的两个实数根,则m2﹣mn+3m+n=( )A、6 B、7 C、8 D、97. 如图,已知二次函数y1=的图象与正比例函数y2=kx(k≠0)的图象相交于点A(3,4),与x轴交于点B(2,0),若0<y1<y2 , 则x的取值范围是( ) A、 B、2<x<3 C、 D、0<x<38. 在平面直角坐标系中,把点P(2,3)绕原点旋转90°得到点P1 , 则点P1的坐标是( )A、(﹣3,2) B、(﹣2,3) C、(﹣2,3)或(2,﹣3) D、(﹣3,2)或(3,﹣2)9. 已知函数y=3﹣(x﹣m)(x﹣n),并且a , b是方程3﹣(x﹣m)(x﹣n)=0的两个根,则实数m , n , a , b的大小关系可能是( )A、m<n<b<a B、m<a<n<b C、a<m<b<n D、a<m<n<b10. 二次函数y=ax2+3x﹣1与x轴的交点个数是( )A、2 B、1 C、0 D、不能确定11. 已知二次函数y=﹣x2+x+6,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线y=﹣x+m与新图象有3个交点时,m的值是( )
A、 B、2<x<3 C、 D、0<x<38. 在平面直角坐标系中,把点P(2,3)绕原点旋转90°得到点P1 , 则点P1的坐标是( )A、(﹣3,2) B、(﹣2,3) C、(﹣2,3)或(2,﹣3) D、(﹣3,2)或(3,﹣2)9. 已知函数y=3﹣(x﹣m)(x﹣n),并且a , b是方程3﹣(x﹣m)(x﹣n)=0的两个根,则实数m , n , a , b的大小关系可能是( )A、m<n<b<a B、m<a<n<b C、a<m<b<n D、a<m<n<b10. 二次函数y=ax2+3x﹣1与x轴的交点个数是( )A、2 B、1 C、0 D、不能确定11. 已知二次函数y=﹣x2+x+6,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线y=﹣x+m与新图象有3个交点时,m的值是( ) A、 B、﹣2 C、﹣2或3 D、﹣6或﹣212. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac﹣b2>8a;④;⑤b>c . 其中含所有正确结论的选项是( )
A、 B、﹣2 C、﹣2或3 D、﹣6或﹣212. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac﹣b2>8a;④;⑤b>c . 其中含所有正确结论的选项是( )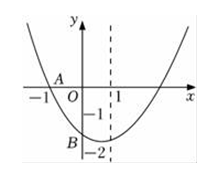 A、①②③ B、②③④ C、①④⑤ D、①③④⑤
A、①②③ B、②③④ C、①④⑤ D、①③④⑤二、填空题(本大题共7小题,每小题4分,共28分.将答案填在答题卡对应的位置上)
-
13. 若一元二次方程x2﹣2x﹣3a=0无实根,则a取值范围是 .14. 若抛物线y=ax2+bx+c过点A(﹣1,2),B(3,2),则此抛物线的对称轴是直线 .15. 如图,△ABC中∠B=50°,在同一平面内,将△ABC绕点A逆时针旋转到△ADE,使AD⊥BC,连接CE,则∠ACE=°.
 16. 如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2﹣mx+c<n的解集是 .
16. 如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2﹣mx+c<n的解集是 . 17. 学校组织一次乒乓球赛,要求每两队之间都要赛一场.若共赛了15场,则有几个球队参赛?设有x个球队参赛,则可列方程为 .18. 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为cm.
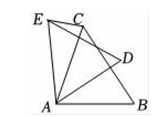
17. 学校组织一次乒乓球赛,要求每两队之间都要赛一场.若共赛了15场,则有几个球队参赛?设有x个球队参赛,则可列方程为 .18. 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为cm. 19. 如图,点O为等边△ABC内一点AO=8,BO=6,CO=10,将△AOC绕点A顺时针方向旋转60°,使AC与AB重合,点O旋转至点O1处,连接OO1 , 则四边形AO1BO的面积是 .
19. 如图,点O为等边△ABC内一点AO=8,BO=6,CO=10,将△AOC绕点A顺时针方向旋转60°,使AC与AB重合,点O旋转至点O1处,连接OO1 , 则四边形AO1BO的面积是 .
三、解答题(本大题共6小题,共74分解答应写出文字说明、证明过程或推演步骤)
-
20. 解方程:(1)、(2x+3)2=(3x+2)2;(2)、3x2+2x﹣5=0;(3)、x2﹣6x+3=0.21. 如图所示,在正方形网格上有一个△ABC .
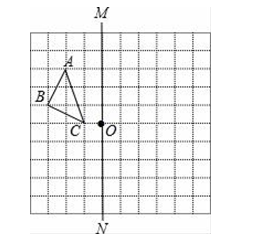 (1)、画出△ABC关于直线MN的对称图形△A1B1C1;(2)、画出△ABC关于点O的对称图形△A2B2C2;(3)、若网格上的最小正方形边长为1,求△ABC的面积;(4)、△A2B2C2能否由△A1B1C1平移得到?能否由△A1B1C1旋转得到?这两个三角形(指
(1)、画出△ABC关于直线MN的对称图形△A1B1C1;(2)、画出△ABC关于点O的对称图形△A2B2C2;(3)、若网格上的最小正方形边长为1,求△ABC的面积;(4)、△A2B2C2能否由△A1B1C1平移得到?能否由△A1B1C1旋转得到?这两个三角形(指△A1B1C1与△A2B2C2)存在什么样的图形变换关系?
22. 先阅读下面的内容,再解决问题.例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+( n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
问题:
(1)、若x2+2y2﹣2xy+4y+4=0,求x2+y2的值.(2)、已知等腰△ABC的三边长为a , b , c , 其中a , b满足:a2+b2+45=12a+6b , 求△ABC的周长.23. 如图,点M,N分别在正方形ABCD的边BC,CD上,且∠MAN=45°.把△ADN绕点A顺时针旋转90°得到△ABE. (1)、求证:△AEM≌△ANM.(2)、若BM=3,DN=2,求正方形ABCD的边长.24. 某宾馆有40个房间供游客居住,当每个房间每天的定价为200元时,房间会全部住满:当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.(1)、若每个房间定价增加30元,则这个宾馆这一天的利润为多少元?(2)、若宾馆某一天获利8400元,则房价定为多少元?(3)、房价定为多少时,宾馆的利润最大?25. 在平面直角坐标系xOy中(如图).已知抛物线y=﹣ x2+bx+c经过点A(﹣1,0)和点B(0, ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)、求证:△AEM≌△ANM.(2)、若BM=3,DN=2,求正方形ABCD的边长.24. 某宾馆有40个房间供游客居住,当每个房间每天的定价为200元时,房间会全部住满:当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.(1)、若每个房间定价增加30元,则这个宾馆这一天的利润为多少元?(2)、若宾馆某一天获利8400元,则房价定为多少元?(3)、房价定为多少时,宾馆的利润最大?25. 在平面直角坐标系xOy中(如图).已知抛物线y=﹣ x2+bx+c经过点A(﹣1,0)和点B(0, ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.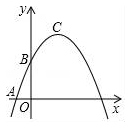 (1)、求这条抛物线的表达式;(2)、求线段CD的长;(3)、将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
(1)、求这条抛物线的表达式;(2)、求线段CD的长;(3)、将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.