安徽省亳州市2023-2024学年九年级上学期第三次月考数学试题
试卷更新日期:2024-01-15 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 如图,在中, , , , , 则的值是( )
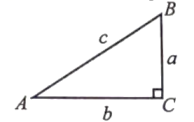 A、 B、 C、 D、2. 若 , 则( )A、 B、 C、 D、3. 在中, , , , 则的值是( )A、 B、 C、 D、4. 如图,在中, , , , 分别在 , 上,将沿翻折后,点落在点处,若为的中点,则折痕的长为( )
A、 B、 C、 D、2. 若 , 则( )A、 B、 C、 D、3. 在中, , , , 则的值是( )A、 B、 C、 D、4. 如图,在中, , , , 分别在 , 上,将沿翻折后,点落在点处,若为的中点,则折痕的长为( ) A、1 B、2 C、3 D、5. 如图,的顶点都是正方形网格中的格点,则等于( )
A、1 B、2 C、3 D、5. 如图,的顶点都是正方形网格中的格点,则等于( )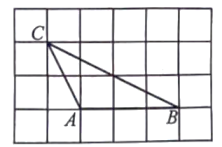 A、 B、 C、 D、6. 已知在中, , , 则的值为( )A、 B、 C、 D、7. 观察下列各式:①;②(是锐角);③ , 其中成立的有( )A、0个 B、1个 C、2个 D、3个8. 在菱形中,是边上的点,连接交于点 , 若 , 则的值是( )A、 B、 C、 D、9. 两个不同的二次函数与的图象有相同的对称轴,则下列结论不正确的是( )A、这两个函数图象的开口方向相反 B、这两个函数图象的都经过点 C、这两个函数图象的关于轴对称 D、二次函数的最大值为10. 如图,在中, , 在边的延长线上取一点 , 过点的直线分别交 , 的延长线于点 , , 则下列结论一定正确的是( )
A、 B、 C、 D、6. 已知在中, , , 则的值为( )A、 B、 C、 D、7. 观察下列各式:①;②(是锐角);③ , 其中成立的有( )A、0个 B、1个 C、2个 D、3个8. 在菱形中,是边上的点,连接交于点 , 若 , 则的值是( )A、 B、 C、 D、9. 两个不同的二次函数与的图象有相同的对称轴,则下列结论不正确的是( )A、这两个函数图象的开口方向相反 B、这两个函数图象的都经过点 C、这两个函数图象的关于轴对称 D、二次函数的最大值为10. 如图,在中, , 在边的延长线上取一点 , 过点的直线分别交 , 的延长线于点 , , 则下列结论一定正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 写一个图象顶点为的二次函数表达式:.12. 已知在中, , , 则的值是.13. 某市为改善交通状况,修建了大量的高架桥.一汽车在坡度为的笔直高架桥起点开始爬行,行驶了15米到达点 , 则此时汽车离地面的高度为米.
 14. 已知二次函数 , 当时,.(1)、若 , , 则.(2)、若抛物线经过点和点 , 则的取值范围是.
14. 已知二次函数 , 当时,.(1)、若 , , 则.(2)、若抛物线经过点和点 , 则的取值范围是.三、(本大题共2小题,每小题8分,满分16分)
-
15. 计算:.16. 在平面直角坐标系中,点 , , 分别位于三个不同象限,若反比例函数的图象经过其中两点,求反比例函数的表达式和的值.
四、(本大题共2小题,每小题8分,满分16分)
-
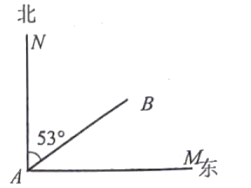
17. 一船自西向东航行,在得到消息,在其北偏东53°方向,距离30海里的点处,测得有一暗礁群在以点为圆心,海里为半径的圆内,问如果轮船继续沿正东方向航行有无触礁的危险?说明理由.(参考数据: , , , )
 18. 如图,在正方形网格内,已知格点 , 点和线段 , 且 , , 都在格点上.
18. 如图,在正方形网格内,已知格点 , 点和线段 , 且 , , 都在格点上. (1)、以点为位似中心,在正方形网格内作的位似图形 , 使与的相似比为;(2)、以为一边,画出一个 , 使.
(1)、以点为位似中心,在正方形网格内作的位似图形 , 使与的相似比为;(2)、以为一边,画出一个 , 使.五、(本大题共2小题,每小题10分,满分20分)
-
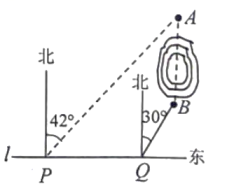
19. 某风景区,水竹亭在紫微阁的正南方向,两个景点被一座小山阻隔,计划在 , 之间修建一条直通景观隧道(如图).为测量 , 两点之间距离,在一条东西方向的公路上选择 , 两点分别观测 , , 已知点在点的北偏东42°方向上,点在点的北偏东30°方向上,米,米,试求 , 两点之间的距离.(参考数据: , , , 其中)
 20. 如图,在中,是边上的一点,且 , , 与相交于点 , 与相交于点.
20. 如图,在中,是边上的一点,且 , , 与相交于点 , 与相交于点.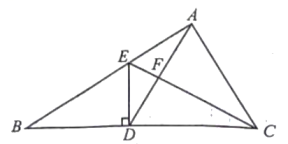 (1)、证明:;(2)、若 , , 求的面积.
(1)、证明:;(2)、若 , , 求的面积.六、(本题满分12分)
-
21. 如图,已知正比例函数和反比例函数的图象交于点.
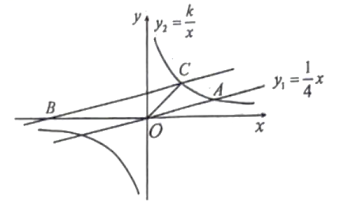 (1)、求反比例函数的表达式;(2)、观察图象,直接写出当时,自变量的取值范围;(3)、将直线沿轴向上平移,使平移后的直线与轴交于 , 与双曲线在第一象限内交于点 , 求点的坐标.
(1)、求反比例函数的表达式;(2)、观察图象,直接写出当时,自变量的取值范围;(3)、将直线沿轴向上平移,使平移后的直线与轴交于 , 与双曲线在第一象限内交于点 , 求点的坐标.七、(本题满分12分)
-
22. 新年即将到来,某电商销售 , 两种学生台历,它们进价相同,种学生台历售价可变,最低售价不能低于进价,最高利润不超过4元,种学生台历售价不变.它们的每本销售利润与每周销售量如下表:(售价进价+利润)
品牌
每本销售利润/元
2
每周销售量/本
当时,
当时,500
(1)、当种学生台历每周销售量为600本时,种学生台历每周销售多少本?(2)、种学生台历每本利润定为多少元时,电商每周销售学生台历可获得最大总利润?并求最大总利润.八、(本题满分14分)
-
23. 在锐角三角形中, , 是高,延长至点 , 再连接并延长,与的延长线交于点 , 已知 , 请你探究:
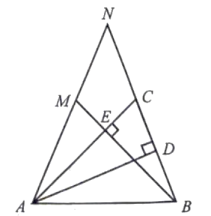 (1)、当时.
(1)、当时.①求的大小(用含的式子表示);
②求证:;
(2)、求的值.
-
-