安徽省宿州市砀山重点中学2023-2024学年七年级上学期月考数学试题
试卷更新日期:2024-01-15 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 先贤孔子曾说过“鼓之舞之”,这是“鼓舞”一词最早的起源,如图是喜庆集会时击鼓瞬间的情景及鼓的立体图形,该鼓从正面看的形状图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 下列四个图中,能用三种方法表示同一个角的是( )A、
2. 下列运算正确的是( )A、 B、 C、 D、3. 下列四个图中,能用三种方法表示同一个角的是( )A、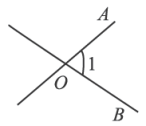 B、
B、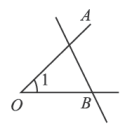 C、
C、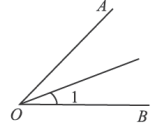 D、
D、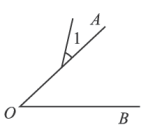 4. 下列变形中,不正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形,则这个多边形是( )A、六边形 B、七边形 C、八边形 D、九边形6. 是下列哪一选项中方程的解( )A、 B、 C、 D、7. 平面上有三点 , 如果 , 那么( )A、点C在线段上 B、点C在线段的延长线上 C、点C在直线外 D、点C可能在直线上,也可能在直线外8. 如图,某小区要绿化一扇形空地,准备在小扇形内种花在其余区域内(阴影部分)种草,测得 , , , 则种草区域的面积为( )
4. 下列变形中,不正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形,则这个多边形是( )A、六边形 B、七边形 C、八边形 D、九边形6. 是下列哪一选项中方程的解( )A、 B、 C、 D、7. 平面上有三点 , 如果 , 那么( )A、点C在线段上 B、点C在线段的延长线上 C、点C在直线外 D、点C可能在直线上,也可能在直线外8. 如图,某小区要绿化一扇形空地,准备在小扇形内种花在其余区域内(阴影部分)种草,测得 , , , 则种草区域的面积为( ) A、 B、 C、 D、9. 在同一平面内有四条直线,每两条直线都相交,则这四条直线的交点共有( )A、6个 B、1个或4个 C、6个或4个 D、1个或4个或6个10. 一条数轴上有点A,B , 点C在线段上,其中点A,B表示的数分别是 , 6,现以点C为折点,将数轴向右对折,若点落在数轴上且与点B的距离为4个单位,则点C表示的数是( )
A、 B、 C、 D、9. 在同一平面内有四条直线,每两条直线都相交,则这四条直线的交点共有( )A、6个 B、1个或4个 C、6个或4个 D、1个或4个或6个10. 一条数轴上有点A,B , 点C在线段上,其中点A,B表示的数分别是 , 6,现以点C为折点,将数轴向右对折,若点落在数轴上且与点B的距离为4个单位,则点C表示的数是( ) A、1 B、 C、或3 D、1或
A、1 B、 C、或3 D、1或二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是 .
 12. 是第五代移动通信技术,其网络下载速度可以达到每秒以上,正常下载一部高清电影约需1秒.将1300000用科学记数法表示为 .13. 已知点C为线段上一点,分别是的中点,则的长为 .14. 由一些正整数组成的数表如下(表中下一行中数的个数是上一行中数的个数的2倍):
12. 是第五代移动通信技术,其网络下载速度可以达到每秒以上,正常下载一部高清电影约需1秒.将1300000用科学记数法表示为 .13. 已知点C为线段上一点,分别是的中点,则的长为 .14. 由一些正整数组成的数表如下(表中下一行中数的个数是上一行中数的个数的2倍):第1行
2
第2行
4 6
第3行
8 10 12 14
…
…
若规定坐标号表示第m行从左向右第n个数,则:
(1)、所表示的数是;(2)、数2024对应的坐标号是 .三、(本大题共2小题,每小题8分,满分16分)
-
15. 如图,已知四个点A、B、C、D,根据下列要求画图:
 (1)、画线段AB;(2)、画∠CDB;(3)、找一点P,使P既在直线AD上,又在直线BC上.16. 化简求值: , 其中 .
(1)、画线段AB;(2)、画∠CDB;(3)、找一点P,使P既在直线AD上,又在直线BC上.16. 化简求值: , 其中 .四、(本大题共2小题,每小题8分,满分16分)
-
17. 计算:(1)、;(2)、 .18. 解方程:(1)、;(2)、 .
五、(本大题共2小题,每小题10分,满分20分)
-
19.(1)、请写出下列展开图中对应几何体的名称:①;②;③ .
 (2)、图③中,侧面展开图的宽(较短边)为 , 圆的半径为 , 求图③所对应几何体的表面积.(结果保留π)20. 某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价48元,乒乓球每盒定价12元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球x盒(不小于5盒).(1)、用代数式表示甲、乙两店购买所需的费用;(2)、当需要40盒乒乓球时,通过计算,说明此时去哪家购买较为合算.
(2)、图③中,侧面展开图的宽(较短边)为 , 圆的半径为 , 求图③所对应几何体的表面积.(结果保留π)20. 某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价48元,乒乓球每盒定价12元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球x盒(不小于5盒).(1)、用代数式表示甲、乙两店购买所需的费用;(2)、当需要40盒乒乓球时,通过计算,说明此时去哪家购买较为合算.六、(本题满分12分)
-
21. 定义:如果两个一元一次方程的解之和为1,我们就称这两个方程为“和谐方程”.例如:方程和为“和谐方程”.(1)、若关于x的方程与方程是“和谐方程”,求m的值;(2)、若关于x的两个方程与是“和谐方程,求m的值.
七、(本题满分12分)
-
22. 如图,是的平分线,是的平分线.
 (1)、如图1,当是直角,时,的度数是多少?(2)、如图2,当时,猜想与的数量关系,并说明理由;(3)、如图3,当时,直接写出的值为 .
(1)、如图1,当是直角,时,的度数是多少?(2)、如图2,当时,猜想与的数量关系,并说明理由;(3)、如图3,当时,直接写出的值为 .八、(本题满分14分)
-
23. 如表是某月的月历.
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
如图所示的三种图形框(图形框①、图形框②、图形框③),可以框住日历中的三个数,设被这三种图形框框住的三个数中最大的数都为x .
 (1)、请用含x的式子表示:
(1)、请用含x的式子表示:第①个图形框中框住的三个数从小到大依次是 , , x;
第②个图形框中框住的三个数从小到大依次是 , , x;
第③个图形框中框住的三个数从小到大依次是 , , x;
(2)、设第①个图形框中三数之和为 , 第②个图形框中三数之和为 , 第③个图形框中三数之和为 , 是否存在这样的x , 使得?若能,请求出的值;若不能,请说明理由.
-
-