安徽省宿州市砀山重点中学2023-2024学年八年级上学期月考数学试题
试卷更新日期:2024-01-15 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 下列方程是二元一次方程的是( )A、 B、 C、 D、2. 用代入消元法解方程组 , 将①代入②可得( )A、 B、 C、 D、3. 在数中,无理数是( )A、 B、0.303003 C、 D、4. 已知是直线上的两个点,则的大小关系是( )A、 B、 C、 D、5. 一次函数和的图象如图所示,则二元一次方程组的解是( )
 A、 B、 C、 D、6. 已知点与点关于轴对称,则的值为( )A、 B、 C、 D、17. 如果一个三角形的三边满足关系式 , 那么这个三角形的形状为( )A、锐角三角形 B、针角三角形 C、直角三角形 D、以上都不对8. 如图,以的三边为直角边分别向外作等腰直角三角形.若 , 则图中阴影部分的面积为( )
A、 B、 C、 D、6. 已知点与点关于轴对称,则的值为( )A、 B、 C、 D、17. 如果一个三角形的三边满足关系式 , 那么这个三角形的形状为( )A、锐角三角形 B、针角三角形 C、直角三角形 D、以上都不对8. 如图,以的三边为直角边分别向外作等腰直角三角形.若 , 则图中阴影部分的面积为( )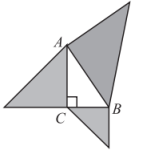 A、6 B、 C、 D、259. 正比例函数的图象如图所示,则一次函数的图象大致是( )
A、6 B、 C、 D、259. 正比例函数的图象如图所示,则一次函数的图象大致是( ) A、
A、 B、
B、 C、
C、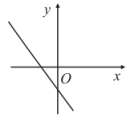 D、
D、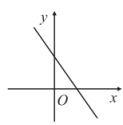 10. 如图1是2023年12月份的月历,小军同学用“
10. 如图1是2023年12月份的月历,小军同学用“ ”字形框在月历上框出四个数字,将该“
”字形框在月历上框出四个数字,将该“ ”字形框上下左右移动,且一定要框住月历中的四个日期,若其中两个日期如图2所示,则m,n的值可能为( )
”字形框上下左右移动,且一定要框住月历中的四个日期,若其中两个日期如图2所示,则m,n的值可能为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 若是关于的二元一次方程的解,则的值为 .12. 在中,若 , 则 .13. 用五个大小完全相同的长方形在直角坐标系中摆成如图所示的图案,若点的坐标为 , 则点的坐标为 .
 14. 如图,直线与轴交于点 , 直线与轴交于点 , 且经过点 , 直线与交于点 .
14. 如图,直线与轴交于点 , 直线与轴交于点 , 且经过点 , 直线与交于点 . (1)、;(2)、点是轴上一动点,连接 , 若的周长最小,则点的坐标为 .
(1)、;(2)、点是轴上一动点,连接 , 若的周长最小,则点的坐标为 .三、(本大题共2小题,每小题8分,满分16分)
-
15. 解下列方程组:(1)、;(2)、 .16. 已知与成正比例,且当时, .(1)、求与之间的函数关系式;(2)、若点在这个函数的图象上,求的值.
四、(本大题共2小题,每小题8分,满分16分)
-
17. 已知方程组 , 由于甲看错了方程①中的 , 得到方程组的解为 , 乙看错了②中的 , 得到方程组的解为 , 若按正确的计算,求原方程组的解.18. 已知点 , 解答下列各题:(1)、点在轴上,求出点的坐标;(2)、若点在第二象限,且它到轴的距离与轴的距离相等,求的值.
五、(本大题共2小题,每小题10分,满分20分)
-
19. 已知一次函数的图象与轴交于点 , 与轴交于点 .
 (1)、求两点的坐标,并画出该函数的图象;(2)、求的长.20. 已知为实数,如果规定一种运算@,即 , 试根据这种运算完成下列各题.(1)、求;(2)、求 .
(1)、求两点的坐标,并画出该函数的图象;(2)、求的长.20. 已知为实数,如果规定一种运算@,即 , 试根据这种运算完成下列各题.(1)、求;(2)、求 .六、(本题满分12分)
-
21. 某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知 , 技术人员通过测量确定了 .
 (1)、小区内部分居民每天必须从点经过点再到点位置,为了方便居民出人,技术人员打算在绿地中开辟一条从点直通点的小路,请问如果方案落实施工完成,居民从点到点将少走多少路程?(2)、这片绿地的面积是多少?
(1)、小区内部分居民每天必须从点经过点再到点位置,为了方便居民出人,技术人员打算在绿地中开辟一条从点直通点的小路,请问如果方案落实施工完成,居民从点到点将少走多少路程?(2)、这片绿地的面积是多少?七、(本题满分12分)
-
22. 某校准备组织七年级400名学生参加夏令营,已知满员时,用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人.(1)、1辆小客车和1辆大客车都坐满后一次可送多少名学生?(2)、若学校计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
①请你设计出所有的租车方案;②若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的租车方案,并求出最少租金.
八、(本题满分14分)
-
23. 在两地之间有服务区 , 甲车由地驶往服务区 , 乙车由地驶往地,两车同时出发,匀速行驶.如图是甲、乙两车分别距离服务区的路程(单位:千米)与乙车行驶时间(单位:小时)之间的函数图象,结合图象信息,解答下列问题:
 (1)、甲车的速度是千米/时;(2)、求图象中线段的函数表达式(要求写出自变量的取值范围);(3)、当两车距服务区的路程之和是360千米时,直接写出此时乙车的行驶时间.
(1)、甲车的速度是千米/时;(2)、求图象中线段的函数表达式(要求写出自变量的取值范围);(3)、当两车距服务区的路程之和是360千米时,直接写出此时乙车的行驶时间.
-
-