贵州省2023-2024九年级上学期数学期末模拟考试试卷（人教版）

试卷更新日期：2024-01-15 类型：期末考试

进入出卷网下载

一、选择题：（本题共10小题，每小题3分，共30分）

1. 下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（　　）

A、戴口罩讲卫生 B、勤洗手勤通风 C、有症状早就医 D、少出门少聚集

查看试题解析
2. 抛物线y=(x+1)²＋2的对称轴是（　　）

A、直线x=－1 B、直线x=1 C、直线y=－1 D、直线y=1

查看试题解析
3. 用配方法解一元二次方程 $x^{2} + 4 x + 1 = 0$ ，下列变形正确的是（）

A、 $(x + 2)^{2} = 3$ B、 $(x + 4)^{2} = 15$ C、 $(x + 2)^{2} = 15$ D、 $(x - 2)^{2} - 3 = 0$

查看试题解析
4. 抛物线y＝ $\frac{1}{2}$ x²向左平移1个单位，再向上平移2个单位后，所得抛物线的表达式是（）

A、y＝ $\frac{1}{2}$ （x+1）²﹣2 B、y＝ $\frac{1}{2}$ （x﹣1）²+2 C、y＝ $\frac{1}{2}$ （x﹣1）²﹣2 D、y＝ $\frac{1}{2}$ （x+1）²+2

查看试题解析
5. 如图， $A B$ 是 $⊙ O$ 弦， $O C ⊥ A B$ 于点 $D$ ，交 $⊙ O$ 于点 $C$ ，若半径为5， $O D = 3$ ，则弦 $A B$ 的长为（）

A、5 B、6 C、7 D、8

查看试题解析
6. 如图，在 $△ A B C$ 中， $A B = 4$ ， $B C = 7.6$ ， $∠ B = 6 0^{∘}$ ，将 $△ A B C$ 绕点 $A$ 顺时针旋转得到 $△ A D E$ ，当点 $B$ 的对应点 $D$ 恰好落在 $B C$ 边上时， $C D$ 的长为（）

A、 $3.6$ B、 $3.8$ C、4 D、 $4.6$

查看试题解析
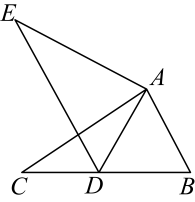7. 若二次函数y＝x²﹣2x＋k的图象经过点（﹣1，y₁），（3，y₂），则y₁与y₂的大小关系为（）

A、y₁＞y₂ B、y₁＝y₂ C、y₁＜y₂ D、不能确定

查看试题解析
8. 如图，在⊙O中，AB是直径，弦AC=5，∠BAC=∠D．则AB的长为（）

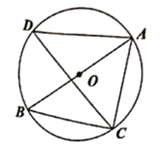A、5 B、10 C、 $5 \sqrt{2}$ D、 $10 \sqrt{2}$

查看试题解析
9.
如图，正六边形ABCDEF中，AB=2，点P是ED的中点，连接AP，则AP的长为（　　）

A、 $2 \sqrt{3}$ B、4 C、 $\sqrt{13}$ D、 $\sqrt{11}$

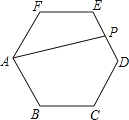查看试题解析
10. 如图为二次函数y＝ax²+bx+c的图象，其对称轴为x＝1，在下列结论中：
①abc＞0；②若方程ax²+bx+c＝0的根是x₁、x₂ ，则x₁+x₂＜0；③4a+2b+c＜0；④当x＞1时，y随x的增大而增大．正确的有（）

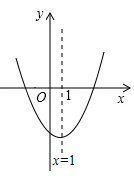A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本题共7小题，每小题4分，共28分）

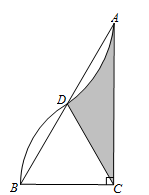
11. 将一元二次方程x²＝1﹣3x化为一般形式是．

查看试题解析
12. 在平面直角坐标系中，点 $M (- 1 ， 2)$ 关于原点对称的点的坐标是．

查看试题解析
13. 李同学掷一枚质地均匀的骰子，点数为2的一面朝上的概率为.

查看试题解析
14. 已知x＝﹣1是方程x²+ax+4＝0的一个根，则方程的另一个根为．

查看试题解析
15. 圆锥底面圆半径为5，母线长为6，则圆锥侧面积等于.

查看试题解析
16. 烟花厂为国庆70周年庆祝晚会特别设计制作一种新型礼炮，这种礼炮的升空高h（m）与飞行时间t（s）的关系式是 $h = - \frac{5}{2} t^{2} + 20 t + 1$ ，若这种礼炮在点火升空到最高点处引爆，则从点火升空到引爆需要时间为.

查看试题解析
17. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 2 \sqrt{3}$ ，以点 $C$ 为圆心， $C B$ 的长为半径画弧，与 $A B$ 边交于点 $D$ ，将 $\overset{⌢}{B D}$ 绕点 $D$ 旋转 $180 °$ 后点 $B$ 与点 $A$ 恰好重合，则图中阴影部分的面积为

查看试题解析

三、解答题（一）：（本题3小题，每题6分，共18分）

18. 解方程： $x^{2} - 2 x - 3 = 0$ .

查看试题解析
19. 已知抛物线的顶点为(-1，-3)，与y轴的交点为(0，-5)求抛物线的解析式.

查看试题解析
20. 如图，在平面直角坐标系中， $△ A B C$ 的顶点均在格点上．

(1)、画出以点 $C$ 为旋转中心，将 $△ A B C$ 绕点 $C$ 顺时针旋转90°得到的 $△ A_{1} B_{1} C$ ；

(2)、写出点 $A_{1}$ 、点 $B_{1}$ 的坐标．

查看试题解析

四、解答题（二）：（本题3小题，每小题8分，共24分）

21. 已知关于 $x$ 一元二次方程 $x^{2} - m x + m - 1 = 0$ .

(1)、求证：方程总有两个实数根；

(2)、若方程有一个根为负数，求 $m$ 的取值范围.

查看试题解析
22. 为决定谁获得仅有的一张电影票，甲和乙设计了如下游戏：在三张完全相同的卡片上，分别写上字母 $A$ ， $B$ ， $B$ ，背面朝上，每次活动洗均匀．
甲说：我随机抽取一张，若抽到字母 $B$ ，电影票归我；
乙说：我随机抽取一张后放回，再随机抽取一张，若两次抽取的字母相同的电影票归我．

(1)、求甲获得电影票的概率；

(2)、求乙获得电影票的概率；

(3)、此游戏对谁有利？

查看试题解析
23. 某商店以每件40元的价格进了一批商品，出售价格经过两个月的调整，从每件50元上涨到每件72元，此时每月可售出188件商品.

(1)、求该商品平均每月的价格增长率；

(2)、因某些原因，商家需尽快将这批商品售出，决定降价出售.经过市场调查发现：售价每下降一元，每个月多卖出一件，设实际售价为x元，则x为多少元时销售此商品每月的利润可达到4000元.

查看试题解析

五、解答题（三）：（本题2小题，每小题10分，共20分）

24. 如图，AB是⊙O的直径，点C、D在⊙O上，且AD平分∠CAB，过点D作AC的垂线，与AC的延长线相交于E，与AB的延长线相交于点F，G为AB的下半圆弧的中点，DG交AB于H，连接DB、GB．

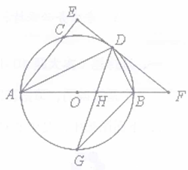(1)、证明EF是⊙O的切线；

(2)、求证：∠DGB=∠BDF：

(3)、已知圆的半径R=5，BH=3，求GH的长．

查看试题解析
25. 如图，在平面直角坐标系中，已知点B坐标为 $(- 1 ， 0)$ ，且 $O A = O C = 4 O B$ ，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 图像经过A ， B ， C三点．

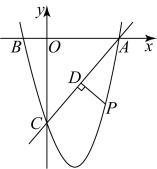(1)、求A ， C两点的坐标；

(2)、求抛物线解析式；

(3)、若点P是直线 $A C$ 下方的抛物线上的一个动点，作 $P D ⊥ A C$ 于点D ，当 $P D$ 的值最大时，求此时点P的坐标及 $P D$ 的最大值．

查看试题解析