河北省石家庄市赵县2023-2024学年八年级上学期第三次月考数学试题

试卷更新日期：2024-01-15 类型：月考试卷

进入出卷网下载

一、选择题（本大题有16个小题，共42分．1~10小题各3分，11~16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的，请用2B铅笔将正确选项涂黑）

1. 下列各组图形中是全等图形的是（）

A、 B、 C、 D、

查看试题解析
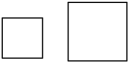2. 用四个螺丝将四条不可弯曲的本条围成一个木框（形状不限），不记螺丝大小，其中相邻两螺丝之间的距离依次为3，4，5，7.且相邻两本条的夹角均可调整，若调整木条的夹角时不破坏此木框，则任意两个螺丝之间的最大距离是（）

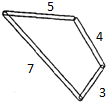A、6 B、7 C、8 D、9

查看试题解析
3. 若64⁴×8³＝2ⁿ ，则n的值是(　　)

A、11 B、18 C、30 D、33

查看试题解析
4. 下列运算中，正确的是（）

A、 $x^{3} + x^{3} = x^{6}$ B、 $x^{3} \cdot x^{9} = x^{27}$ C、 ${(x^{2})}^{3} = x^{5}$ D、 $x \div x^{2} = x^{- 1}$

查看试题解析
5. 如果一个正方体的棱长是 ${(a + b)}^{3}$ ，那么这个正方体的体积是（）

A、 ${(a + b)}^{6}$ B、 $6 {(a + b)}^{6}$ C、 ${(a + b)}^{9}$ D、 ${(a + b)}^{12}$

查看试题解析
6. 如图， $A B = C D$ ， $D E = A F$ ， $C F = B E$ ， $∠ A F B = 80 °$ ， $∠ C D E = 60 °$ ，那么 $∠ A B C =$ （）

A、 $80 °$ B、 $60 °$ C、 $40 °$ D、 $20 °$

查看试题解析
7. 在螳螂的示意图中，AB∥DE，△ABC是等腰三角形，∠ABC＝124°，∠CDE＝72°，则∠ACD＝（）

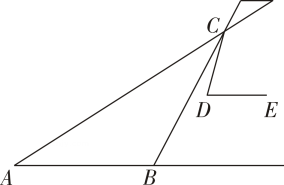A、16° B、28° C、44° D、45°

查看试题解析
8. 如图，在 $△$ ABC中，D是BC上的点，且BD＝2，DC＝1， $S_{△ A C D}$ ＝12，那么 $S_{△ A B C}$ 等于（）

A、30 B、36 C、72 D、24

查看试题解析
9. 使 $(x^{2} + p x + 8) (x^{2} - 3 x + q)$ 乘积中不含 $x^{2}$ 与 $x^{3}$ 项的p，q的值是（）

A、 $p = 0$ ， $q = 0$ B、 $p = 3$ ， $q = 1$ C、 $p = - 3$ ， $q = - 9$ D、 $p = - 3$ ， $q = 1$

查看试题解析
10. 如图，已知 $△ A B C$ ，求作一点 $P$ ，使点 $P$ 到 $∠ A$ 两边的距离相等，且 $P A = P B$ ，下列确定点 $P$ 的方法正确的是（）

A、点 $P$ 是 $∠ A$ 与 $∠ B$ 的平分线与 $A B$ 的垂直平分线的交点 B、点 $P$ 为 $∠ A$ 的平分线与 $A B$ 的垂直平分线的交点 C、点 $P$ 为 $A C$ ， $A B$ 两边上的高的交点 D、点 $P$ 为 $A C$ ， $A B$ 两边的垂直平分线的交点

查看试题解析
11. 若（x－5）(x＋2)＝x²＋px＋q ，则p、q的值是（　）

A、3，10 B、3，-10 C、-3，10 D、-3，-10

查看试题解析
12. 将多项式4x²+1再加上一项，使它能分解因式成（a+b）²的形式，以下是四位学生所加的项，其中错误的是（）

A、2x B、﹣4x C、4x⁴ D、4x

查看试题解析
13. 以下说法中，正确的个数有（　　）
①三角形的内角平分线、中线、高都是线段；
②三角形的三条高一定都在三角形的内部；
③三角形的一条中线将此三角形分成两个面积相等的小三角形；
④三角形的3个内角中，至少有2个角是锐角．

A、1 B、2 C、3 D、4

查看试题解析
14. 如图，已知BE＝CE ， ED为△EBC的中线，BD＝8，△AEC的周长为24，则△ABC的周长为(　　)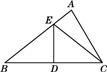

A、40 B、46 C、50 D、56

查看试题解析
15. 如图，AD∥BC，∠ABC的平分线BP与∠BAD的平分线AP相交于点P，作PE⊥AB于点E.若PE＝3，则两平行线AD与BC间的距离为（）

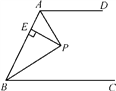A、3 B、4 C、5 D、6

查看试题解析
16. 观察下面图形，从图1到图2可用式子表示为（）

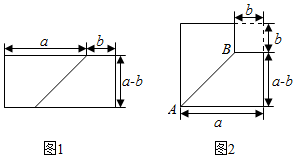A、（a+b）（a﹣b）＝a²﹣b² B、a²﹣b²＝（a+b）（a﹣b） C、（a+b）²＝a²+2ab+b² D、a²+2ab+b²＝（a+b）²

查看试题解析

二、填空题（本大题有3个小题，每小题有2个空，每空2分，共12分）

17. 把多项式 $x^{2} + a x + b$ 分解因式，得 $(x + 1) (x - 3)$ ，则 $a =$ ， $b =$ ．

查看试题解析
18. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ C A B$ ， $D E ⊥ A B$ 于点 $E$ ，已知 $A C = 6$ ， $B C = 8$ ， $C D = 3$ ，则 $D E =$ ， $S_{△ A D B} =$ ．

查看试题解析
19. 观察下列等式：①9-1=8，②16-4=12，③25-9=16，④36-16=20，…写出第10个等式：，第n(n≥1)个式子是.

查看试题解析

三、解答题（本大题共7个小题，共66分．解答应写出文字说明、证明过程或演算步骤）

20.

(1)、已知 $2^{x} = 2$ ， $2^{y} = 4$ 求 $2^{x + y}$ 的值；

(2)、已知 $x^{2 n} = 5$ ，求 ${(3 x^{3 n})}^{2} - 4 {(x^{2})}^{2 n}$ 的值．

查看试题解析
21. 把下列各式因式分解：

(1)、 $x^{3} - 4 x$ ；

(2)、 $2 x^{2} - 12 x y + 18 y^{2}$ ；

(3)、 $x^{2} (x - 2) + (2 - x)$ ．

查看试题解析
22. 在 $△$ ABC中，已知点D，E，F分别为边BC，AD，CE的中点．

(1)、如图1，若 $S_{△ A B C}$ ＝1cm² ，求 $△$ BEF的面积．

(2)、如图2，若 $S_{△ B F C}$ ＝1cm² ，则 $S_{△ A B C}$ ＝．

查看试题解析
23. 如图， $A B = A C$ ， $D B = D C$ ， $E B = E C$ ．

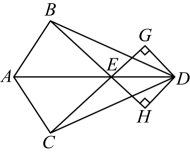(1)、图中有几对全等三角形？请一一写出来．

(2)、过点 $D$ 作 $D H ⊥ B E$ ， $D G ⊥ C E$ ，垂足分别为 $H$ ， $G$ ．求证： $D G = D H$ ．

查看试题解析
24. 请认真观察图形，解答下列问题：

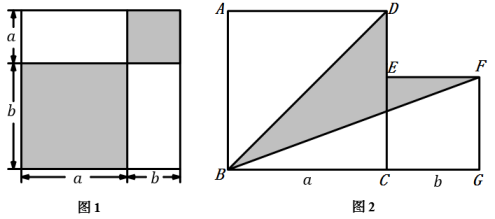(1)、根据图 $1$ 中条件，试用两种不同方法表示两个阴影图形的面积的和．
方法 $1$ ：，方法 $2$ ：；

(2)、从中你能发现什么结论？请用等式表示出来：；

(3)、利用(2)中结论解决下面的问题：如图 $2$ ，两个正方形边长分别为 $a$ ， $b$ ，如果 $a + b = 6 ， a b = 8$ ，求阴影部分的面积．

查看试题解析
25. 问题：如图，在△ABD中，BA=BD，在BD的延长线上取点E，C，作△AEC，使EA=EC。若∠BAE=90°，∠B=45°，求∠DAC的度数。
答案：∠DAC=45°。

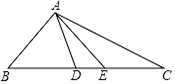
思考：

(1)、如果把以上“问题”中的条件“∠B=45°”去掉，其余条件不变，那么∠DAC的度数会改变吗？说明理由。

(2)、如果把以上“问题”中的条件“∠B=45°”去掉，再将“∠BAE=90°”改为“∠BAE=n°”，其余条件不变，求∠DAC的度数。

查看试题解析
26. 如图，在平面直角坐标系中 $A (a ， 0) ， B (0 ， b)$ ，满足 $a^{2} - 4 a + 4 + | b - 4 | = 0$

(1)、求 $A ， B$ 两点的坐标；

(2)、 $∠ O B A$ 的平分线 $B C$ 与 $∠ O A B$ 的外角平分线AM交于点C，求 $∠ C$ 的度数；

(3)、在平面内是否存在点P，使 $Δ A B P$ 为等腰直角三角形？若存在，请写出点P的个数，并直接写出其中两个点的坐标；若不存在，请说明理由.

查看试题解析