河北省石家庄市赵县重点学校2023-2024学年九年级上学期月考数学试题
试卷更新日期:2024-01-15 类型:月考试卷
一、选择题(本大题共16个小题,共38分.1~6小题各3分;7~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列关系式中,是的反比例函数的是( )A、 B、 C、 D、2. 下列各点在反比例函数的图象上的点是( )A、 B、 C、 D、3. 若 , 则的值为( )A、 B、 C、3 D、14. 如果两个相似三角形的面积比是1:4,那么它们的周长比是( )A、1:16 B、1:4 C、1:6 D、1:25. 如图,四边形和相似,则和的大小分别为( )
 A、 30 B、 33 C、 30 D、 336. 若双曲线的图象经过第二、四象限,则的取值范围是( )A、 B、 C、 D、不存在7. 下列格点三角形中,与图中格点相似的是( )
A、 30 B、 33 C、 30 D、 336. 若双曲线的图象经过第二、四象限,则的取值范围是( )A、 B、 C、 D、不存在7. 下列格点三角形中,与图中格点相似的是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,身高为的琪琪想测量学校旗杆的高度,当她站在处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得 , , 则旗杆的高度是( )
8. 如图,身高为的琪琪想测量学校旗杆的高度,当她站在处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得 , , 则旗杆的高度是( ) A、 B、 C、 D、9. 在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:)是体积(单位:)的反比例函数,其图象如图所示,当时,气体的密度是( )
A、 B、 C、 D、9. 在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:)是体积(单位:)的反比例函数,其图象如图所示,当时,气体的密度是( ) A、 B、 C、 D、10. 若 , 两点均在函数的图象上,且 , 则与的大小关系为( )A、 B、 C、 D、11. 下面的四个问题中都有两个变量与 , 变量与之间的函数关系可以用如图所示的图象表示的是( )
A、 B、 C、 D、10. 若 , 两点均在函数的图象上,且 , 则与的大小关系为( )A、 B、 C、 D、11. 下面的四个问题中都有两个变量与 , 变量与之间的函数关系可以用如图所示的图象表示的是( ) A、汽车以一定的速度匀速行驶,汽车行驶的路程与行驶时间 B、用长度一定的绳子围成一个矩形,矩形的面积与一边长 C、三角形的面积一定,它的一边与这边上的高 D、等腰三角形的周长一定,它的底边与腰长12. 如图,已知 , 那么添加下列一个条件后,仍无法判定的是( )
A、汽车以一定的速度匀速行驶,汽车行驶的路程与行驶时间 B、用长度一定的绳子围成一个矩形,矩形的面积与一边长 C、三角形的面积一定,它的一边与这边上的高 D、等腰三角形的周长一定,它的底边与腰长12. 如图,已知 , 那么添加下列一个条件后,仍无法判定的是( ) A、 B、 C、 D、13. 在平面直角坐标系中,线段两个端点的坐标分别为 , , 以原点为位似中心,在第三象限内将线段缩小为原来的后得到线段 , 则点的对应点的坐标为( )A、 B、 C、 D、14. 如图,在平面直角坐标系中,点为坐标原点,点和点都在坐标轴上,若反比例函数的图象经过矩形的对称中心,则的值为( )
A、 B、 C、 D、13. 在平面直角坐标系中,线段两个端点的坐标分别为 , , 以原点为位似中心,在第三象限内将线段缩小为原来的后得到线段 , 则点的对应点的坐标为( )A、 B、 C、 D、14. 如图,在平面直角坐标系中,点为坐标原点,点和点都在坐标轴上,若反比例函数的图象经过矩形的对称中心,则的值为( )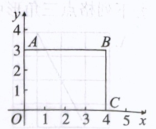 A、3 B、 C、1.5 D、15. 已知反比例函数与正比例函数的一个交点坐标为 , 则另一个交点坐标为( )A、 B、 C、 D、16. 如图,在中,为的中点,连接交于点 , 射线与射线交于点 .
A、3 B、 C、1.5 D、15. 已知反比例函数与正比例函数的一个交点坐标为 , 则另一个交点坐标为( )A、 B、 C、 D、16. 如图,在中,为的中点,连接交于点 , 射线与射线交于点 .结论Ⅰ:;结论Ⅱ: .
对上面两个结论,下列说法正确的是( )
 A、结论Ⅰ正确,结论Ⅱ错误 B、结论Ⅱ正确,结论Ⅰ错误 C、两个结论都正确 D、两个结论都错误
A、结论Ⅰ正确,结论Ⅱ错误 B、结论Ⅱ正确,结论Ⅰ错误 C、两个结论都正确 D、两个结论都错误二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分,把答案写在题中横线上)
-
17. 已知反比例函数的图象分布在第二、四象限,则在一次函数中,随的增大而(选填“增大”“减小”或“不变”).18. 如图,为测量小河两岸、两点之间的距离,在小河一侧选出一点 , 使点在点正南方,在点正东方,过点作 , 垂足为 , 测得 , , 根据所学知识可证得(写出一个即可),根据所测得的数据可算出、两点之间的距离是 .
 19. 如图,点 , 是双曲线上的点,过 , 两点分别向轴、轴作垂线,垂足分别为点 , , , , , 交于点 .
19. 如图,点 , 是双曲线上的点,过 , 两点分别向轴、轴作垂线,垂足分别为点 , , , , , 交于点 .
⑴若 , , 则;
⑵若四边形是矩形,四边形是正方形,且 , , 则正方形的边长为 .
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20. 根据下列条件,判断与是否相似,并说明理由.(1)、 , , , , , ;(2)、 , , , .21. 已知反比例函数(为常数,)的图象经过点 .(1)、求这个函数的解析式;(2)、判断点 , 是否在这个函数的图象上,并说明理由;(3)、当时,求的取值范围.22. 如图,在四边形中, , 点为的中点, .
 (1)、求证:;(2)、若 , , 求线段、的长.23. 如图,一次函数的图象与反比例函数的图象交于、两点.
(1)、求证:;(2)、若 , , 求线段、的长.23. 如图,一次函数的图象与反比例函数的图象交于、两点. (1)、求反比例函数和一次函数的解析式;(2)、求的面积;(3)、当时,根据图象直接写出的取值范围.24. 如图,三个顶点的坐标分别为 , , , 以原点为位似中心,将放大为原来的2倍得到 .
(1)、求反比例函数和一次函数的解析式;(2)、求的面积;(3)、当时,根据图象直接写出的取值范围.24. 如图,三个顶点的坐标分别为 , , , 以原点为位似中心,将放大为原来的2倍得到 .
 (1)、在图中第一象限内画出符合要求的;(不要求写画法)(2)、计算的面积;(3)、内有一点 , 内与点对应的点的坐标为 .25. 已知一艘轮船上装有120吨货物,轮船到达目的地后开始卸货.设平均卸货速度为(单位:吨/小时),卸完这批货物所需的时间为(单位:小时).(1)、求关于的函数表达式;(2)、若要求不超过6小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?(3)、按6小时卸完船上的这批货物,卸货2小时后,根据实际情况,要求剩下的货物要在2小时内卸完,在剩下的时间内每小时要多卸多少吨货物?26. 如图,在中, , , , 现有动点从点出发,沿向点方向运动,速度是 , 动点在线段上运动.它们同时出发,当有一点到达终点,另一点也停止运动.设运动时间为 .
(1)、在图中第一象限内画出符合要求的;(不要求写画法)(2)、计算的面积;(3)、内有一点 , 内与点对应的点的坐标为 .25. 已知一艘轮船上装有120吨货物,轮船到达目的地后开始卸货.设平均卸货速度为(单位:吨/小时),卸完这批货物所需的时间为(单位:小时).(1)、求关于的函数表达式;(2)、若要求不超过6小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?(3)、按6小时卸完船上的这批货物,卸货2小时后,根据实际情况,要求剩下的货物要在2小时内卸完,在剩下的时间内每小时要多卸多少吨货物?26. 如图,在中, , , , 现有动点从点出发,沿向点方向运动,速度是 , 动点在线段上运动.它们同时出发,当有一点到达终点,另一点也停止运动.设运动时间为 . (1)、若点从点出发,沿向点方向运动,速度为 .
(1)、若点从点出发,沿向点方向运动,速度为 .①在运动过程中,始终平行于 , 则 ▲ ;
②在①的条件下,当时, , 两点之间的距离是多少?
(2)、若点从点出发,沿向点方向运动,速度是 . 当为多少秒时,以点 , , 为顶点的三角形与相似?