浙教版数学八下同步练习：2.3 一元二次方程的应用

试卷更新日期：2024-01-14 类型：同步测试

进入出卷网下载

一、选择题

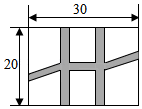
1. 把一元二次方程（1﹣x）（2﹣x）=3﹣x²化成一般形式ax²+bx+c=0（a≠0）其中a、b、c分别为（　　）

A、2、3、﹣1 B、2、﹣3、﹣1 C、2、﹣3、1 D、2、3、1

查看试题解析
2. 某商店对一种商品进行库存清理，第一次降价 $30 %$ ，销量不佳；第二次又降价 $10 %$ ，销售大增，很快就清理了库存．设两次降价的平均降价率为x，下面所列方程正确的是（）

A、 $\frac{300 + 10 %}{2} = x$ B、 $(1 - 30 %) (1 - 10 %) = (1 - 2 x)$ C、 $(1 - 30 %) (1 - 10 %) = 2 (1 - x)$ D、 $(1 - 30 %) (1 - 10 %) = {(1 - x)}^{2}$

查看试题解析
3. 某商店将进货价格为20元的商品按单价36元售出时，能卖出200个．已知该商品单价每上涨1元，其销售量就减少5个．设这种商品的售价上涨 $x$ 元时，获得的利润为1200元，则下列关系式正确的是（　　）

A、 $(x + 16) (200 - 5 x) = 1200$ B、 $(x + 16) (200 + 5 x) = 1200$ C、 $(x - 16) (200 + 5 x) = 1200$ D、 $(x - 16) (200 - 5 x) = 1200$

查看试题解析
4. 如图，某小区居民休闲娱乐中心是建在一块长方形（长30米，宽20米）场地，被 $3$ 条宽度相等的绿化带划分为总面积为480平方米的6块活动场所．如果想求绿化带的宽度 $x$ 米，可列出的方程为（）

A、 $(30 - x) (20 - x) = 480$ B、 $(30 - 2 x) (20 - 2 x) = 480$ C、 $(30 - 2 x) (20 - x) = 480$ D、 $(30 - x) (20 - 2 x) = 480$

查看试题解析
5. $2023$ 年 $4$ 月 $23$ 是第 $28$ 个世界读书日，读书已经成为很多人的一种生活方式，城市书院是读书的重要场所之一，据统计，某书院对外开放的第一个月进书院 $600$ 人次，进书院人次逐月增加，到第三个月末累计进书院 $2850$ 人次，若进书院人次的月平均增长率为 $x$ ，则可列方程为（）

A、 $600 (1 + 2 x) = 2850$ B、 $600 {(1 + x)}^{2} = 2850$ C、 $600 + 600 (1 + x) + 600 {(1 + x)}^{2} = 2850$ D、 $2850 {(1 - x)}^{2} = 600$

查看试题解析

二、填空题

6. 一个两位数，十位上的数字比个位上的数字的平方少9.如果把十位上的数字与个位上的数字对调，得到的两位数比原来的两位数小27，则原来的两位数是

查看试题解析
7. 某市某企业为节约用水，自建污水净化站.7月份净化污水6000吨，9月份增加到7260吨，则这两个月净化的污水量平均每月增长的百分率为．

查看试题解析
8. 某商场将进价为30元的台灯以单价40元售出，平均每月能售出600个．调查表明：这种台灯的单价每上涨1元，其销售量将减少10个．为实现平均每月10000元的销售利润，从消费者的角度考虑，商场对这种台灯的售价应定为元．

查看试题解析
9. 一商店销售某种商品，平均每天可售出20件，每件盈利40元，为了扩大销售、增加盈利，该店采取了1降价措施，经过一段时间的销售，发现销售单价每降低1元，平均每天可多售出2件.当每件商品降价多少元时，该商店每天销售利润为1200元？若设降价x元，可列方程为.

查看试题解析
10. 如图，是一个长为30m，宽为20m的矩形花园，现要在花园中修建等宽的小道，剩余的地方种植花草.如图所示，要使种植花草的面积为468m² ，那么小道进出口的宽度应为 m.

查看试题解析

三、解答题

11. 如图是一个三角点阵，从上向下数有无数多行，其中第一行有 $1$ 个点，第二行有 $2$ 个点 $\dots .$ 第 $n$ 行有 $n$ 个点 $\dots$ ．

(1)、根据上面的内容，请直接写出 $10$ 是三角点阵中前行的点数和；

(2)、请直接写出三角点阵中前 $8$ 行的点数和；

(3)、三角点阵中前 $n$ 行的点数和能是 $136$ 吗？如果能，请求出 $n$ ，如果不能，请说明理由；

(4)、如果把图 $1$ 的三角点阵中各行的点数依次换为 $2$ ， $4$ ， $6$ ， $\dots$ ， $2 n$ ， $\dots$ ，你能探究出前 $n$ 行的点数和满足什么规律吗？这个三角点阵中前 $n$ 行的点数和能是 $650$ 吗？如果能，请求出 $n$ ，如
果不能，请说明理由．

查看试题解析
12. 某工厂一种产品2013年的产量是100万件，计划2015年产量达到121万件，假设2013年到2015年这种产品产量的年增长率相同，求2013年到2015年这种产品产量的年增长率．

查看试题解析
13. 某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利40元，为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件。

(1)、若商场想平均每天盈利1200元，每件衬衫应降价多少元？

(2)、商场有可能每天平均盈利1300元吗？若有可能，应降价多少元？

查看试题解析
14. 某社区在开展“美化社区，幸福家园”活动中，计划利用如图所示的直角墙角 $($ 阴影部分，两边足够长 $)$ ，用 $50$ 米长的篱笆围成一个矩形花园 $A B C D ($ 篱笆只围 $A B$ ， $A D$ 两边 $)$ ．

(1)、若花园的面积为 $400$ 平方米，求 $A B$ 的长；

(2)、若在直角墙角内点 $P$ 处有一棵桂花树，且与墙 $B C$ ， $C D$ 的距离分别是 $10$ 米， $30$ 米，要将这棵树围在矩形花园内 $($ 含边界，不考虑树的粗细 $)$ ，则花园的面积能否为 $625$ 平方米？若能，求出 $A B$ 的值；若不能，请说明理由．

查看试题解析
15. 某水果批发商店以每千克 $12$ 元的价格购进一批水果，然后以每千克 $15$ 元的价格出售，一天可售出 $100$ 千克．通过调查发现，每千克的售价每降低 $0.1$ 元，一天可多售出 $20$ 千克．

(1)、若将这种水果每千克的售价降低 $x$ 元，则一天的销售量是克；（用含 $x$ 的代数式表示）

(2)、要想一天盈利 $500$ 元，且保证一天销售量不少于 $280$ 千克，商店需将每千克的售价降低多少元？

查看试题解析

四、综合题

16. 端午节前夕，某超市从厂家分两次购进蛋黄粽子、红豆粽子，两次进货时，两种粽子的进价不变．第一次购进蛋黄粽子60袋和红豆粽子90袋，总费用为4800元；第二次购进蛋黄粽子40袋和红豆粽子80袋，总费用为3600元．

(1)、求蛋黄粽子、红豆粽子每袋的进价各是多少元？

(2)、当蛋黄粽子销售价为每袋70元时；每天可售出20袋，为了促销，该超市决定对蛋黄粽子进行降价销售．经市场调研，若每袋的销售价每降低1元，则每天的销售量将增加5袋．当蛋黄粽子每袋的销售价为多少元时，每天售出蛋黄粽子所获得的利润为220元？

查看试题解析
17. 如图，在矩形 $A B C D$ 中， $A B = 16 cm$ ， $B C = 6 cm$ ，动点P、Q分别以 $3 cm/s$ ， $2 cm/s$ 的速度从点A ， C同时出发，沿规定路线移动．

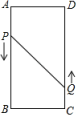
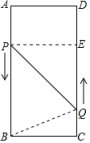(1)、若点P从点A移动到点B停止，点Q随点P的停止而停止移动，问经过多长时间P ， Q两点之间的距离是 $10 cm$ ？

(2)、若点P沿着 $A B \to B C \to C D$ 移动，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间 $△ P B Q$ 的面积为 $12 {cm}^{2}$ ？

查看试题解析