【B卷】第三章 圆—北师大版九年级下册单元测试
试卷更新日期:2024-01-14 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,AB为⊙O的直径,P为BA延长线上的一点,D在⊙O上(不与点A,点B重合),连结PD交⊙O于点C,且PC=OB.设∠P=α,∠B=β,下列说法正确的是( )
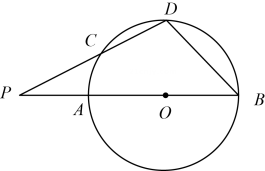 A、α+β=90° B、3α+2β=180° C、5α+4β=180° D、β-α=30°2. 下列命题中,正确的命题是( )A、三角形的外心是三角形三边中垂线的交点 B、三点确定一个圆 C、平分一条弦的直径一定垂直于弦 D、相等的两个圆心角所对的两条弧相等3. 一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.6米,最深处水深0.1米,则此输水管道的半径是( )米
A、α+β=90° B、3α+2β=180° C、5α+4β=180° D、β-α=30°2. 下列命题中,正确的命题是( )A、三角形的外心是三角形三边中垂线的交点 B、三点确定一个圆 C、平分一条弦的直径一定垂直于弦 D、相等的两个圆心角所对的两条弧相等3. 一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.6米,最深处水深0.1米,则此输水管道的半径是( )米 A、1 B、0.8 C、0.6 D、0.54. 如图,点O是外接圆的圆心,点I是的内心,连接 , . 若 , 则的度数为( )
A、1 B、0.8 C、0.6 D、0.54. 如图,点O是外接圆的圆心,点I是的内心,连接 , . 若 , 则的度数为( ) A、 B、 C、 D、5. 如图,四边形ABCD是半圆O的内接四边形,AB是直径,C是的中点.若∠C=110°,则∠ABC的度数为( )
A、 B、 C、 D、5. 如图,四边形ABCD是半圆O的内接四边形,AB是直径,C是的中点.若∠C=110°,则∠ABC的度数为( ) A、55° B、60° C、65° D、75°6. 如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A、55° B、60° C、65° D、75°6. 如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( ) A、 B、 C、 D、7. 如图,一个零刻度落在点A的量角器(半圆O),其直径为AB , 一等腰直角三角板MNB绕点B旋转,斜边BN交半圆O于点C , BM交半圆O于点D , 点C在量角器上的读数为.关于结论Ⅰ,Ⅱ,下列判断正确的是( )
A、 B、 C、 D、7. 如图,一个零刻度落在点A的量角器(半圆O),其直径为AB , 一等腰直角三角板MNB绕点B旋转,斜边BN交半圆O于点C , BM交半圆O于点D , 点C在量角器上的读数为.关于结论Ⅰ,Ⅱ,下列判断正确的是( )结论Ⅰ:;
结论Ⅱ:当边MN与半圆O相切于点E(点E在量角器上的读数为)时,
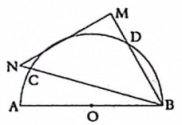 A、只有结论Ⅰ对 B、只有结论Ⅱ对 C、结论Ⅰ、Ⅱ都对 D、结论Ⅰ、Ⅱ都不对8. 如图,的内切圆与 , , 分别相切于点 , , , 若的半径为 , , 则的值和的大小分别为( )
A、只有结论Ⅰ对 B、只有结论Ⅱ对 C、结论Ⅰ、Ⅱ都对 D、结论Ⅰ、Ⅱ都不对8. 如图,的内切圆与 , , 分别相切于点 , , , 若的半径为 , , 则的值和的大小分别为( )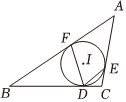 A、 , B、 , C、 , D、 ,9. 我国魏晋时期数学家刘微在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为( )
A、 , B、 , C、 , D、 ,9. 我国魏晋时期数学家刘微在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为( )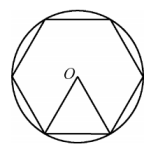 A、 B、 C、3 D、10. 如图所示,已知在平面直角坐标系中,点A,B的坐标分别为 , 点是轴正半轴上的一点,且满足 , 现有以下4个结论:①的外接圆的圆心在OC上;②∠ABC=60°;③△ABC的外接圆的半径等于;④.其中正确的是( ).
A、 B、 C、3 D、10. 如图所示,已知在平面直角坐标系中,点A,B的坐标分别为 , 点是轴正半轴上的一点,且满足 , 现有以下4个结论:①的外接圆的圆心在OC上;②∠ABC=60°;③△ABC的外接圆的半径等于;④.其中正确的是( ).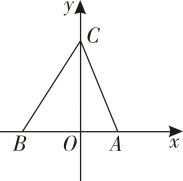 A、①② B、②③ C、③④ D、①④
A、①② B、②③ C、③④ D、①④二、填空题(每题3分,共15分)
-
11. 如图,在矩形ABCD中,AB=3,AD=6,点E、F分别是AB、BC边上的动点,且AE:BF=2:1,连接AF和DE交于点G , 连接CG , 则CG的最小值是 .
 12. 如图所示的网格由边长均为1的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则外接圆的圆心是点 , 弧的长是.
12. 如图所示的网格由边长均为1的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则外接圆的圆心是点 , 弧的长是.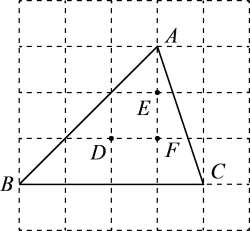 13. 已知一次函数的图像经过第一、二、四象限,以坐标原点O为圆心、r为半径作 . 若对于符合条件的任意实数k,一次函数的图像与总有两个公共点,则r的最小值为 .14. 如图,扇形纸片的半径为2,沿折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为.
13. 已知一次函数的图像经过第一、二、四象限,以坐标原点O为圆心、r为半径作 . 若对于符合条件的任意实数k,一次函数的图像与总有两个公共点,则r的最小值为 .14. 如图,扇形纸片的半径为2,沿折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为. 15. 量角器和三角板是我们平常数学学习中常用的工具.有一天,爱思考的小聪拿着两块工具拼成了如图1的样子,计划让三角板的直角顶点始终在量角器的半圆弧上运动,紧接着小聪根据自己的想法画出了示意图(如图2)。已知点C是量角器半圆弧的中点,点P为三角板的直角顶点,两直角边PE、PF分别过点A、B.连结CP,过点O作OM⊥CP交CP于点M,交AP于点N若AB=8,则NB的最小值为;若点Q为的中点,则点P从点Q运动到点B时,N点的运动路径长为.
15. 量角器和三角板是我们平常数学学习中常用的工具.有一天,爱思考的小聪拿着两块工具拼成了如图1的样子,计划让三角板的直角顶点始终在量角器的半圆弧上运动,紧接着小聪根据自己的想法画出了示意图(如图2)。已知点C是量角器半圆弧的中点,点P为三角板的直角顶点,两直角边PE、PF分别过点A、B.连结CP,过点O作OM⊥CP交CP于点M,交AP于点N若AB=8,则NB的最小值为;若点Q为的中点,则点P从点Q运动到点B时,N点的运动路径长为.
三、作图题(共7分)
-
16. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , .
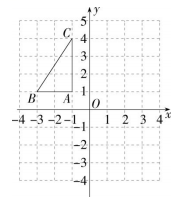 (1)、的外接圆的半径为;(2)、将绕点B顺时针旋转后得到 , 请在图中画出;(3)、在(2)的条件下,求出点C经过的路径长.
(1)、的外接圆的半径为;(2)、将绕点B顺时针旋转后得到 , 请在图中画出;(3)、在(2)的条件下,求出点C经过的路径长.四、解答题(共7题,共68分)
-
17. 平面内有A,B,C,D四个点,试探索:(1)、若四点共线,则过其中三点作圆,可作个圆.(2)、若有三点共线,则过其中三点作圆,可作个圆.(3)、若任意三点不共线,则过其中三点作圆,可作个圆.(4)、过A,B,C,D四个点中的任意三点作圆,最多可以作几个圆?最少可以作几个圆?18. 如图,△OAB中,OA=OB=10cm , ∠AOB=80°,以点O为圆心,半径为6cm的优弧 分别交OA、OB于点M、N .
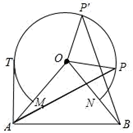 (1)、点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;(2)、点T在左半弧上,若AT与圆弧相切,求AT的长.(3)、Q为优弧上一点,当△AOQ面积最大时,请直接写出∠BOQ的度数为 .19. 定义:若圆内接三角形是等腰三角形,我们就称这样的三角形为“圆等三角形”.
(1)、点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;(2)、点T在左半弧上,若AT与圆弧相切,求AT的长.(3)、Q为优弧上一点,当△AOQ面积最大时,请直接写出∠BOQ的度数为 .19. 定义:若圆内接三角形是等腰三角形,我们就称这样的三角形为“圆等三角形”. (1)、如图1,AB是⊙O的一条弦(非直径),若⊙O在上找一点C,使得△ABC是“圆等三角形”,则这样的点C能找到个.(2)、如图2,四边形ABCD是⊙O的内接四边形,连结对角线BD,△ABD和△BCD均为“圆等三角形”,且AB=AD.
(1)、如图1,AB是⊙O的一条弦(非直径),若⊙O在上找一点C,使得△ABC是“圆等三角形”,则这样的点C能找到个.(2)、如图2,四边形ABCD是⊙O的内接四边形,连结对角线BD,△ABD和△BCD均为“圆等三角形”,且AB=AD.①当∠A=140°时,求∠ADC的度数;
②如图3,当∠A=120°,AB=6时,求阴影部分的面积.
20. 【我们画不出一个完美的圆,但完美的圆是存在的,虽不能至,心向往之罗翔】已知四边形是半径为的内接四边形,弦的长度是 , 点是劣弧上的一个动点.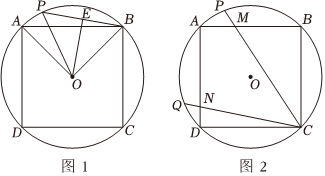 (1)、填空:的度数是 ,并判断平行四边形是否会是正方形 填“是”或“不是”;(2)、如图 , 若点是弦的中点,连接 , , 当点沿着劣弧从点开始,顺时针运动到点时,求的外心所经过的路径的长度;(3)、如图 , 点是劣弧另一个动点,并始终满足 , 、分别交弦 , 于点、 , 连接记的面积为 , 的面积为 , 的面积为 .
(1)、填空:的度数是 ,并判断平行四边形是否会是正方形 填“是”或“不是”;(2)、如图 , 若点是弦的中点,连接 , , 当点沿着劣弧从点开始,顺时针运动到点时,求的外心所经过的路径的长度;(3)、如图 , 点是劣弧另一个动点,并始终满足 , 、分别交弦 , 于点、 , 连接记的面积为 , 的面积为 , 的面积为 .直接写出 , , 之间的数量关系;不必进行证明
令 , , 若满足 , 求 , 的值.
21. 【问题背景】如图 , 在中,将劣弧沿弦所在的直线折叠,使得劣弧恰好过圆心 , 圆心关于直线的对称点为 . (1)、【探究发现】如图 , 连接、 , 并延长交于 , 连接直接写出的度数为 ,与的数量关系为 ;(2)、【深入探究】如图 , 将劣弧沿弦所在的直线折叠,弧不经过圆心 , 在劣弧上取一点不与、重合 , 连接并延长交于点 , 连接、猜想与的数量关系,并说明理由;(3)、【拓展应用】如图 , 在条件下,若平分 , , , 求的长.22. 小明在学习了《圆周角定理及其推论》后,有这样的学习体会:在中, , 当长度不变时.则点C在以为直径的圆上运动(不与A、B重合).
(1)、【探究发现】如图 , 连接、 , 并延长交于 , 连接直接写出的度数为 ,与的数量关系为 ;(2)、【深入探究】如图 , 将劣弧沿弦所在的直线折叠,弧不经过圆心 , 在劣弧上取一点不与、重合 , 连接并延长交于点 , 连接、猜想与的数量关系,并说明理由;(3)、【拓展应用】如图 , 在条件下,若平分 , , , 求的长.22. 小明在学习了《圆周角定理及其推论》后,有这样的学习体会:在中, , 当长度不变时.则点C在以为直径的圆上运动(不与A、B重合).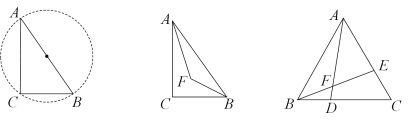 (1)、【探索发现】
(1)、【探索发现】小明继续探究,在中, , 长度不变.作与的角平分线交于点F,小明计算后发现的度数为定值,小明猜想点F也在一个圆上运动.请你计算的度数,并简要说明小明猜想的圆的特征.
(2)、【拓展应用】
在【探索发现】的条件下,若 , 求出面积的最大值.(3)、【灵活运用】
在等边中, , 点D、点E分别在和边上,且 , 连接交于点F,试求出周长的最大值.23. 综合与实践车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆,车轮都是圆形的.为什么车轮要做成圆形的呢?这里面有什么数学道理吗?带着这样的疑问,小青做了如下的探究活动:
将车轮设计成不同的正多边形,在水平地面上模拟行驶.
 (1)、探究一:将车轮设计成等边三角形,转动过程如图1,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图2中计算C到的距离.(2)、探究二:将车轮设计成正方形,转动过程如图3,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图4中计算C到的距离(结果保留根号).(3)、探究三:将车轮设计成正六边形,转动过程如图5,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),在图6中计算C到的距离(结果保留根号).(4)、归纳推理:比较 , , 大小: , 按此规律推理,车轮设计成的正多边形边数越多,其中心轨迹最高点与转动一次前后中心连线(水平线)的距离(填“越大”或“越小”).(5)、得出结论:将车轮设计成圆形,转动过程如图7,其中心(即圆心)的轨迹与水平地面平行,此时中心轨迹最高点与转动前后中心连线(水平线)的距离.这样车辆行驶平稳、没有颠簸感.所以,将车轮设计成圆形.
(1)、探究一:将车轮设计成等边三角形,转动过程如图1,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图2中计算C到的距离.(2)、探究二:将车轮设计成正方形,转动过程如图3,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图4中计算C到的距离(结果保留根号).(3)、探究三:将车轮设计成正六边形,转动过程如图5,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),在图6中计算C到的距离(结果保留根号).(4)、归纳推理:比较 , , 大小: , 按此规律推理,车轮设计成的正多边形边数越多,其中心轨迹最高点与转动一次前后中心连线(水平线)的距离(填“越大”或“越小”).(5)、得出结论:将车轮设计成圆形,转动过程如图7,其中心(即圆心)的轨迹与水平地面平行,此时中心轨迹最高点与转动前后中心连线(水平线)的距离.这样车辆行驶平稳、没有颠簸感.所以,将车轮设计成圆形.
-