【A卷】第三章 圆—2023-2024学年北师大版九年级下册单元测试
试卷更新日期：2024-01-14 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 下列结论不正确的是（ ）A、圆心也是圆的一部分 B、一个圆中最长的弦是直径 C、圆是轴对称图形 D、等弧所在的圆一定是等圆或同圆2. 如图，为的切线，B为切点，交于点C ， 点D在优弧上，若 ， 则的度数为（ ）
A、 B、 C、 D、3. 如图，在⊙O中，直径AB⊥CD，若∠COB=65°，则∠BAD的度数是（ ）
A、25° B、65° C、32.5° D、50°4. 如图，四边形ABCD为 的内接四边形，已知 ，则 的度数为（ ）
A、40° B、50° C、80° D、100°5. 若一个三角形的三边长为6，8，10，则这个三角形外接圆的半径是（ ）A、3 B、4 C、5 D、66. 如图，、分别与相切于A、B两点，且 ， 若点C是上异于点A ， B的一点，则的大小为（ ）
A、 B、 C、或 D、或7. 如图， 、 切 于点 、 ，点 是 上一点，且 ，则 的大小是（ ）
A、 B、 C、 D、8. 如图，正五边形内接于 ， 其半径为1，作交于点F，则的长为（ ）
A、 B、 C、 D、9. 如图，⊙O的半径为5，是△ABC的外接圆．若∠ABC=25°，则劣弧AC的长为（ ）．
A、 B、 C、 D、10. 如图，的半径是 ， 点是直线上一动点，过点作的切线，切点为 ， 连接 ， ， 则的最小值为（ ）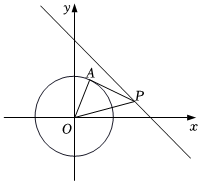
A、 B、 C、 D、二、填空题（每题3分，共15分）
-
11. 已知⊙O的半径为4cm，OP =2cm，则点P在⊙O（填“内"、“外”或“上”）．12. 《九章算术》是中国传统数学重要的著作之一，其中第九卷《勾股》中记载了一个“圆材埋壁”的问题：“今有圆材，埋在壁中，不知大小．以锯锯之、深一寸，锯道长一尺，问径几何？”用几何语言表达为：如图，AB是⊙O的直径，弦CD⊥AB于点E ， EB＝1寸，CD＝10寸，则直径AB长为 寸．
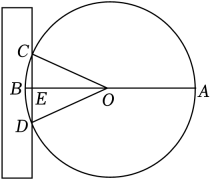13. 如图，点A ， B ， C在⊙O上，∠ACB＝30°，则∠ABO的度数是 ．
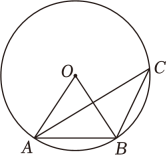14. 已知的半径是一元二次方程的一个根，圆心O到直线l的距离为4，则直线l与有个交点．15. 如图所示，在△ABC中，∠ACB=90°，AC=BC=2.将△ABC绕着点A顺时针旋转90度到△AB1C1的位置，则边BC扫过区域(阴影部分)的面积为(结果用含π的式子表示).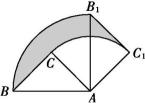
三、解答题（共8题，共55分）
-
16. 如图，正方形网格中的每个小正方形的边长都是1，的三个顶点都在格点上，将绕点A按顺时针方向旋转90°得到.
(1)、在正方形网格中，画出；(2)、求出点C经过的路线长度；(3)、计算线段在变换到的过程中扫过区域的面积.17. 如图，四边形ABCD内接于⊙O，E为BC延长线上的一点，点C为的中点．若∠DCE＝110°，求∠BAC的度数．
18. 有一辆载有集装箱的卡车，高2.5米，宽1.6米，要开进如图所示的上边是半圆，下边是长方形的桥洞，已知半圆的直径为2米，长方形的另一条边长是2.3米，这辆卡车能否通过此桥洞？通过计算说明理由.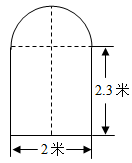
19. 如图，正六边形ABCDEF为⊙O的内接正六边形，连结AE，⊙O的半径为2cm．
(1)、求∠AED的度数和弧AB的长．(2)、求正六边形ABCDEF与⊙O的面积之比．20. 如图，⊙O是△ABC的外接圆，连接OA，过点C作一条射线CD．
(1)、请从以下条件中：①CD∥AO，∠ABC=45°；②∠BCD=∠BAC；③CB平分∠ACD．选择一组能证明CD是⊙O的切线的条件，并写出证明过程；(2)、若OA=2，∠OAB=22.5°，AB=CB，求的长度．(结果保留π)21. 如图，AB是圆O的直径，PB，PC是圆O的两条切线，切点分别为B，C．延长BA，PC相交于点D．
(1)、求证：∠CPB=2∠ABC．(2)、设圆O的半径为2，sin ∠PBC= ，求PC的长．22. 如图，与等边的边、分别交于点、 ， 是的直径，过点作于点 ．
(1)、求证：是的切线：(2)、已知的半径为3，连接 ， 当等边的边长为多少时，与相切？23. 操作与探究我们知道：过任意一个三角形的三个顶点能作一个圆，探究过四边形四个顶点作圆的条件．
(1)、分别测量图1、2、3各四边形的内角，如果过某个四边形的四个顶点能一个圆，那么其相对的两个角之间有什么关系？证明你的发现．
(2)、如果过某个四边形的四个顶点不能一个圆，那么其相对的两个角之间有上面的关系吗？试结合图4、5的两个图说明其中的道理．（提示：考虑∠B+∠D与180°之间的关系）
由上面的探究，试归纳出判定过四边形的四个顶点能作一个圆的条件．