【提升卷】3.9弧长及扇形的面积—2023-2024学年北师大版九年级下册同步测试

试卷更新日期：2024-01-14 类型：同步测试

进入出卷网下载

一、选择题

1. 如图所示，有一边长为6 cm的等边三角形ABC木块，点P是CA的延长线上的点，AP为15 cm，其中 $\overset{⏜}{P D}$ ， $\overset{⏜}{D F}$ ， $\overset{⏜}{F E}$ 的圆心依次为A，B，C，则曲线PDFE的长是（）

A、18π cm B、15π cm C、20π cm D、21π cm

查看试题解析
2. 一块等边三角形木板，边长为1，现将木板沿水平线翻滚(如图)，那么点B从开始至结束所经过的路径长为（）．

A、 $\frac{3 π}{2}$ B、 $\frac{4 π}{3}$ C、4 D、2+ $\frac{3 π}{2}$

查看试题解析
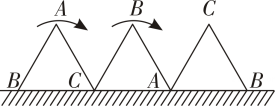3. 如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠B=135° ，则 $\overset{⌢}{A C}$ 的长为（）．

A、2π B、π C、 $\frac{π}{2}$ D、 $\frac{π}{3}$

查看试题解析
4. 某仿古墙上原有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图所示，已知矩形的宽为 $2 m$ ，高为 $2 \sqrt{3} m$ ，则改建后门洞的圆弧长是（）.

A、 $\frac{5 π}{3} m$ B、 $\frac{8 π}{3} m$ C、 $\frac{10 π}{3} m$ D、 $(\frac{5 π}{3} + 2) m$

查看试题解析
5. 如图，扇形 $O A B$ 中， $∠ A O B = 110 ° ， O A = 18 ， C$ 是 $O B$ 的中点， $C D ⊥ O B$ 交 $A B$ 于点 $D$ ，以 $O C$ 为半径的 $C E$ 交 $O A$ 于点 $E$ ，则图中阴影部分的面积是（）

A、 $12 π + 18 \sqrt{3}$ B、 $\frac{81 (\sqrt{3} + 2 π)}{2}$ C、 $\frac{81 (2 \sqrt{3} + π)}{4}$ D、 $6 π + 36 \sqrt{3}$

查看试题解析
6. 某班计划在劳动实践基地内种植蔬菜，班长买回来10米长的围栏，准备围成两边靠墙（两墙垂直且足够长）的菜园，为了让菜园面积尽可能大，同学们提出了围成矩形、等腰直角三角形（两直角边靠墙）、扇形这三种方案，如图所示．最佳方案是（）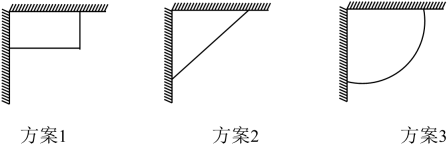

A、方案1 B、方案2 C、方案1或方案2 D、方案3

查看试题解析
7. 如图，在Rt△ABC中，∠ACB=90°，AB= $\sqrt{5}$ ， BC=2，以点A为圆心，AC的长为半径画弧，交AB于点D，交AC于点C，以点B为圆心，AC的长为半径画弧，交AB于点E，交BC于点F则图中阴影部分的面积为（）

A、8-π B、4-π C、2- $\frac{π}{4}$ D、1- $\frac{π}{4}$

查看试题解析
8. 如图，以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点，交直角边AC于点E，且B，E是半圆弧的三等分点．若 $\overset{⌢}{A B}$ 的长为 $\frac{4 π}{3}$ ，则图中阴影部分的面积为（）．

A、 $6 \sqrt{3} - \frac{4 π}{3}$ B、 $9 \sqrt{3} - \frac{8 π}{3}$ C、 $\frac{3 \sqrt{3}}{2} - \frac{2 π}{3}$ D、 $6 \sqrt{3} - \frac{8 π}{3}$

查看试题解析

二、填空题

9. 抖空竹在我国有着悠久的历史，是国家级的非物质文化遗产之一 $.$ 如图， $A C$ ， $B D$ 分别与 $⊙ O$ 相切于点 $C$ ， $D$ ，延长 $A C$ ， $B D$ 交于点 $P .$ 若 $∠ P = 120 °$ ， $⊙ O$ 的半径为 $6 c m$ ，则图中 $\overset{⌢}{C D}$ 的长为 $c m . ($ 结果保留 $π)$

查看试题解析
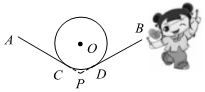10. 如图，等腰 $R t △ A B C$ 中， $A B = A C = \sqrt{2}$ ，以A为圆心，以AB为半径作 $\overset{⌢}{B D C}$ ﹔以BC为直径作 $\overset{⌢}{C A B}$ ．则图中阴影部分的面积是．（结果保留 $π$ ）

查看试题解析
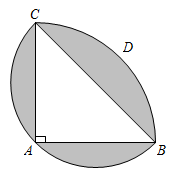11. 如图，有一个半径为2的圆形时钟，其中每个刻度间的弧长均相等，过9点和11点的位置作一条线段，则钟面中阴影部分的面积为．

查看试题解析
12. 已知正六边形的边长为4cm，分别以它的三个不相邻的顶点为圆心，边长为半径作弧(如图)，则所得到的三条弧的长度之和为cm．(结果保留π)

查看试题解析

三、作图题

13. 如图，在平面直角坐标系 $x O y$ 中，点 $A (- 2 ， 0)$ ， $B (0 ， 2)$ ， $\overset{⏜}{A B}$ 所在圆的圆心为 $O .$ 将 $\overset{⏜}{A B}$ 向右平移5个单位，得到 $\overset{⏜}{C D}$ (点A平移后的对应点为C）．

(1)、点 $D$ 的坐标是， $\overset{⏜}{C D}$ 所在圆的圆心坐标是；

(2)、在图中画出 $\overset{⏜}{C D}$ ，并连接 $A C$ ， $B D$ ；

(3)、求由 $\overset{⏜}{A B}$ ， $B D$ ， $\overset{⏜}{D C}$ ， $C A$ 首尾依次相接所围成的封闭图形的周长.（结果保留π）

查看试题解析
14. 如图所示，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点均在格点上，在建立平面直角坐标系后，点C的坐标为（-2，-2）．

(1)、以原点O为对称中心，画出△ABC关于原点O对称的△A₁B₁C₁；

(2)、画出（1）中△A₁B₁C₁以C₁为旋转中心，逆时针旋转90°得到的△A₂B₂C₁ ，并写出点A₂的坐标；

(3)、在（2）的条件下，求旋转过程中边C₁A₁扫过的面积．

查看试题解析

四、解答题

15. 如图，以 $A B$ 为直径的 $⊙ O$ 经过 $A C$ 的中点 $D$ ， $D E ⊥ B C$ 于点 $E$ ．

(1)、求证： $D E$ 是 $⊙ O$ 的切线；

(2)、当 $A B = 4$ ， $∠ C = 30 °$ 时，求图中阴影部分的面积 $($ 结果保留根号和 $π)$ ．

查看试题解析
16. 将一物体(视为边长为 $\frac{2}{π} m$ 的正方形 $A B C D)$ 从地面PQ上挪到货车车厢内.如图所示，刚开始点 $B$ 与斜面EF上的点 $E$ 重合，先将该物体绕点 $B (E)$ 按逆时针方向旋转至正方形 $A_{1} B C_{1} D_{1}$ 的位置，再将其沿EF方向平移至正方形 $A_{2} B_{2} C_{2} D_{2}$ 的位置(此时点 $B_{2}$ 与点 $G$ 重合)，最后将物体移到车厢平台面MG上.已知 $M G / / P Q ， ∠ F B P = 3 0^{°}$ ，过点 $F$ 作 $F H ⊥ M G$ 于点H，FH $= \frac{1}{3} m ， E F = 4 m$ .求：

(1)、线段FG的长度.

(2)、此过程中点A运动至点 $A_{2}$ 所经过的路程.

查看试题解析
17. 图1是某型号汤碗，截面如图2所示，碗体部分为半圆O ，直径 $A B = 20 c m$ ，倒汤时， $∠ C A B = 60 °$ ，如图3所示．

(1)、 $∠ C O B$ 的度数为；

(2)、在图3中，通过计算比较直径 $A B$ 与 $\overset{⌢}{C B}$ 的长度哪个更长；

(3)、请在图3中画出线段 $M N$ ，用其长度表示汤（阴影部分）的最大深度（不说理由），并求汤的最大深度．

查看试题解析
18. 如图1，在正方形ABCD中， $A B = 8$ ，点O与点B重合，以点O为圆心，作半径长为5的半圆O ，交AB于点E ，交AB的延长线于点F ，点M ， N是 $\overset{⌢}{E F}$ 的三等分点（点M在点N的左侧）.将半圆O绕点E逆时针旋转，记旋转角为 $α (0 ° < α \leq 90 °)$ ，旋转后，点F的对应点为点 $F^{'}$ .
图1 图2 备用图

(1)、如图2，在旋转过程中，当 $E F^{'}$ 经过点N时.
①求 $α$ 的度数；
②求图中阴影部分的面积；

(2)、在旋转过程中，若半圆O与正方形ABCD的边相切，请直接写出点A到切点的距离.

查看试题解析