【培优卷】3.9弧长及扇形的面积—北师大版数学九年级下册同步测试
试卷更新日期:2024-01-14 类型:同步测试
一、选择题
-
1. 如图,在矩形中,是边上的一个动点,连结 , 点关于直线的对称点为 , 当运动时,也随之运动.若从运动到 , 则点经过的路径长是( )
 A、 B、 C、 D、2. 已知点A,B,C在⊙O上,∠ABC=30°,把劣弧沿着直线CB折叠交弦AB于点D.若BD=9,AD=6,则的长为( )
A、 B、 C、 D、2. 已知点A,B,C在⊙O上,∠ABC=30°,把劣弧沿着直线CB折叠交弦AB于点D.若BD=9,AD=6,则的长为( ) A、π B、3π C、π D、π3. 已知在扇形中, , , 为弧的中点,为半径上一动点,点关于直线的对称点为 , 若点落在扇形内不含边界 , 则长的取值范围是( )
A、π B、3π C、π D、π3. 已知在扇形中, , , 为弧的中点,为半径上一动点,点关于直线的对称点为 , 若点落在扇形内不含边界 , 则长的取值范围是( ) A、 B、 C、 D、4. 如图,在矩形中, , , 点、分别是边、的中点,某一时刻,动点从点出发,沿方向以每秒2个单位长度的速度向点匀速运动;同时,动点从点出发,沿方向以每秒1个单位长度的速度向点匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接 , 过点作的垂线,垂足为.在这一运动过程中,点所经过的路径长是( )
A、 B、 C、 D、4. 如图,在矩形中, , , 点、分别是边、的中点,某一时刻,动点从点出发,沿方向以每秒2个单位长度的速度向点匀速运动;同时,动点从点出发,沿方向以每秒1个单位长度的速度向点匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接 , 过点作的垂线,垂足为.在这一运动过程中,点所经过的路径长是( )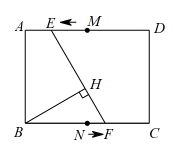 A、 B、 C、 D、5. 如图,四边形是的内接正方形,直线且平分 , 交于点 , 若 , 则阴影部分面积为( )
A、 B、 C、 D、5. 如图,四边形是的内接正方形,直线且平分 , 交于点 , 若 , 则阴影部分面积为( ) A、 B、 C、 D、6. 如图,在边长为4的正六边形中,先以点B为圆心,的长为半径作 , 再以点A为圆心,的长为半径作交于点P,则图中阴影部分的面积为( )
A、 B、 C、 D、6. 如图,在边长为4的正六边形中,先以点B为圆心,的长为半径作 , 再以点A为圆心,的长为半径作交于点P,则图中阴影部分的面积为( ) A、 B、 C、 D、7. 如图,中, , , BO=2cm,将绕点O逆时针旋转至 , 点在BO的延长线上,则边BC扫过区域(图中阴影部分)的面积为( )
A、 B、 C、 D、7. 如图,中, , , BO=2cm,将绕点O逆时针旋转至 , 点在BO的延长线上,则边BC扫过区域(图中阴影部分)的面积为( ) A、 B、 C、 D、8. 如图,正方形ABCD的边长是 , 以正方形对角线的一半OA为边作正六边形,其中一边与正方形的边CD交于点E,再以点O为圆心OE为半径画弧交AD于点F,则图中阴影部分的的面积为( )
A、 B、 C、 D、8. 如图,正方形ABCD的边长是 , 以正方形对角线的一半OA为边作正六边形,其中一边与正方形的边CD交于点E,再以点O为圆心OE为半径画弧交AD于点F,则图中阴影部分的的面积为( )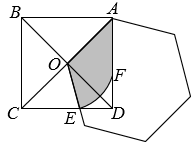 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,正六边形的边长为2,以为圆心,的长为半径画弧,得 , 连接 , , 则图中阴影部分的面积为 .
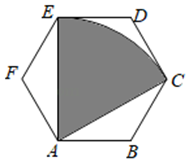 10. 如图,在菱形ABCD中,点E是AB的中点,以B为圆心,BE为半径作弧,交BC于F,连接DE、DF.若AB=2,∠A=60°,则阴影部分的面积为
10. 如图,在菱形ABCD中,点E是AB的中点,以B为圆心,BE为半径作弧,交BC于F,连接DE、DF.若AB=2,∠A=60°,则阴影部分的面积为 11. 如图,已知是△ABC的外接圆,且圆心O在线段AB上,点D是上一点,DA的延长线与过点C的切线交于点E,且 , 连接CD交AB于点F,①若 , 的半径 , 则;②若 , 则.
11. 如图,已知是△ABC的外接圆,且圆心O在线段AB上,点D是上一点,DA的延长线与过点C的切线交于点E,且 , 连接CD交AB于点F,①若 , 的半径 , 则;②若 , 则. 12. 如图,四边形ABCD是边长为的正方形,曲线DA1B1C1D1A2 …是由多段90°的圆心角所对的弧组成的.其中,弧DA1的圆心为A,半径为AD;弧A1B1的圆心为B,半径为BA1;弧B1C1的圆心为C,半径为CB1;弧C1D1的圆心为D,半径为DC1….弧DA1、弧A1B1、弧B1C1、弧C1D1…的圆心依次按点A,B,C,D循环,则弧C2022D2022的长是(结果保留π).
12. 如图,四边形ABCD是边长为的正方形,曲线DA1B1C1D1A2 …是由多段90°的圆心角所对的弧组成的.其中,弧DA1的圆心为A,半径为AD;弧A1B1的圆心为B,半径为BA1;弧B1C1的圆心为C,半径为CB1;弧C1D1的圆心为D,半径为DC1….弧DA1、弧A1B1、弧B1C1、弧C1D1…的圆心依次按点A,B,C,D循环,则弧C2022D2022的长是(结果保留π).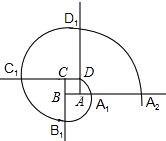
三、解答题
-
13. 如图①,在Rt△ABC中,∠C=90°,∠A=60°,AC=3cm,边AB在直线l上.将Rt△ABC沿直线l作无滑动翻滚,当Rt△ABC翻滚一周时,求点A经过的路径长要解决这个问题,先要弄清在翻滚时点A经过的路径是什么Rt△ABC翻滚一周即为翻滚三次,第一次翻滚点A经过的路径长是以点B为圆心、AB为半径、圆心角是150°的的长,即为5πcm;第二次翻滚点A经过的路线长是以点C1为圆心、A1C1为半径圆心角是90°的的长,即为πcm;第三次翻滚时点A没动.所以Rt△ABC翻滚一周点A经过的路径是5π+π=π(cm).
思考:如图②,在矩形ABCD中,AB=4,BC=3,边CD在直线l上.将矩形ABCD沿直线l作无滑动翻滚,当点A第一次翻滚到点A1位置时,求点A经过的路径长.
 14. 小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作 , 连接BF.
14. 小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作 , 连接BF. (1)、求k的值;(2)、求扇形AOC的半径及圆心角的度数;(3)、请直接写出图中阴影部分面积之和.15. 项目化学习:车轮的形状.
(1)、求k的值;(2)、求扇形AOC的半径及圆心角的度数;(3)、请直接写出图中阴影部分面积之和.15. 项目化学习:车轮的形状.【问题提出】车轮为什么要做成圆形, 这里面有什么数学原理?
(1)、【合作探究】

探究 组:如图1,圆形车轮半径为 ,其车轮轴心 到地面的距离始终为 .
探究 组:如图2,正方形车轮的轴心为 ,若正方形的边长为 ,求车轮轴心 最高点与最低点的高度差.
探究 组:如图3, 有一个破损的圆形车轮, 半径为 ,破损部分是一个弓形,其所对圆心角为 ,其车轮轴心为 ,让车轮在地上无滑动地滚动一周,求点 经过的路程.探究发现:车辆的平稳关键看车轮轴心是否稳定.
(2)、【拓展延伸】如图4,分别以正三角形的三个顶点 为圆心,以正三角形的边长为半径作 圆弧,这个曲线图形叫做“莱洛三角形”.
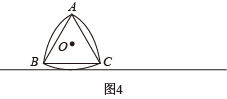
探究 组:使 “莱洛三角形” 沿水平方向向右滚动,在滚动过程中,其每时每刻都有 “最高点”,“中心点” 也在不断移动位置,那么在 “莱洛三角形” 滚动一周的过程中,其“最高点”和“中心点”所形成的图案大致是 .
延伸发现:“莱洛三角形”在滚动时始终位于一组平行线之间,因此放在其上的物体也能够保持平衡,但其车轴中心 并不稳定.