【基础卷】3.9弧长及扇形的面积—2023-2024学年北师大版九年级下册同步测试

试卷更新日期：2024-01-14 类型：同步测试

进入出卷网下载

一、填空题

1. 一条圆弧和经过这条圆弧两端的两条所围成的图形叫作扇形．

查看试题解析
2. 在半径为R的圆中，n°的圆心角所对的弧长l的计算公式为：， l，n，R中，已知两个量，就可以求出第三个量．已知l，n，则R=；已知l，R，则n= ．

查看试题解析
3.

(1)、已知圆的半径为4cm，则120°的圆心角所对的弧长为.

(2)、已知圆弧长为2πcm，弧的度数为40°，则弧所在圆的半径为.

(3)、已知圆弧长为6πcm，弧所在圆的半径为6cm，则弧所对圆周角的度数为.

查看试题解析
4.

(1)、半径为3cm，圆心角为45的扇形面积是.

(2)、弧长为6πcm，半径为5cm的扇形面积是.

查看试题解析
5. 扇形的圆心角为80°，弧长为4πcm，则此扇形的面积等于cm² ．

查看试题解析
6. 已知扇形的面积为12πcm² ，圆心角为120°，则扇形所在圆的半径是.

查看试题解析
7. 已知⊙O的半径为12，则长为6π的弧所对的圆心角度数为

查看试题解析
8. 已知扇形的圆心角为80°，半径为2，则该扇形的弧长为．（结果保留π ）

查看试题解析

二、选择题

9. 如图，AB为半圆的直径，其中AB=4，半圆绕点B顺时针旋转45°，点A旋转到点A’的位置，则图中阴影部分的面积为（）

A、π B、2π C、 $\frac{π}{2}$ D、4π

查看试题解析
10. 如图，一块含有 $30 °$ 角的直角三角板 $A B C$ ，在水平桌面上绕点 $C$ 按顺时针方向旋转到 $A^{'} B^{'} C$ 的位置．若 $B C$ 的长为 $7.5 c m$ ，那么顶点A从开始到结束所经过的路径长为（）

A、 $10 π c m$ B、 $10 \sqrt{3} π c m$ C、 $15 π c m$ D、 $20 π c m$

查看试题解析
11. 如图，△ABC内接于半径为2的⊙O．若∠A=45°，则 $\overset{⌢}{B C}$ 的长等于（）

A、 $\frac{1}{4}$ π B、 $\frac{1}{2}$ π C、π D、2π

查看试题解析
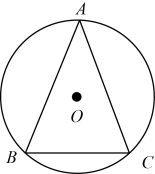12. 已知圆心角为120°的扇形的弧长为6π，该扇形的面积为（）

A、 $18 π$ B、 $27 π$ C、 $36 π$ D、 $54 π$

查看试题解析
13. 如图，正五边形 $A B C D E$ 内接于半径为3的 $⊙ O$ ，则阴影部分的面积为（）

A、 $\frac{18 π}{5}$ B、 $\frac{12 π}{5}$ C、 $\frac{9 π}{5}$ D、 $\frac{6 π}{5}$

查看试题解析
14. 如图是2022年杭州亚运会徽标的示意图，若AO＝5，BO＝2，∠AOD＝120°，则阴影部分面积为（）

A、14π B、2π C、 $\frac{25}{3} π$ D、7π

查看试题解析
15. 如图，以AB为直径，点O为圆心的半圆经过点C．若AC=BC=2，则图中阴影部分的面积是（）．

A、 $\frac{π}{4}$ B、 $\frac{1}{2} + \frac{π}{4}$ C、 $\frac{π}{2}$ D、 $\frac{1}{2} + \frac{π}{2}$

查看试题解析
16. 如图所示，在半径1的圆形纸片中，剪一个圆心角为 $9 0^{°}$ 的扇形(图中阴影部分)，则这个扇形的面积为（）.

A、 $\frac{1}{2} π$ B、 $π$ C、 $\frac{3}{2} π$ D、 $\frac{\sqrt{2}}{4} π$

查看试题解析

三、解答题

17. 如图，△ABC是⊙O的内接三角形，AD是⊙O的直径，且AD=6，∠ABC=∠CAD．求弦AC所对的弧长．

查看试题解析
18. 如图，在△ABC中，AB=4cm，∠B=30°，∠ACB=45°．以A为圆心，AC长为半径作弧，与AB交于点E，与BC交于点F．求 $\overset{⌢}{C E}$ 的长．

查看试题解析
19. 如图所示的图形叫弧三角形，又叫莱洛三角形，是机械学家莱洛首先进行研究的．弧三角形是这样画的：先画正三角形ABC，然后分别以点A，B，C为圆心，AB长为半径画弧．若正三角形ABC的边长为2cm，求弧三角形的周长．

查看试题解析
20. 如图，在△ABC中，AB=BC=2，∠ABC=90，求图中阴影部分的面积．

查看试题解析
21. 已知：如图，A，B，C是⊙O上的三点，且 $\overset{⌢}{A B}$ =2 $\overset{⌢}{B C}$ ．过点B作BD⊥OC于点D．

(1)、求证：AB=2BD．

(2)、若AB= $2 \sqrt{3}$ ， CD=1，求图中阴影部分的面积．

查看试题解析
22. 如图，半圆O的直径AB=10．将半圆O绕点B顺时针旋转45°得到半圆O'，与AB交于点P．

(1)、求AP的长．

(2)、求图中阴影部分的面积．(结果保留π)

查看试题解析
23. 如图，△ABC与△A'B'C是两个可以完全重合的直角三角板，∠B=30°，AB=10cm．将三角板A'B'C绕直角顶点C顺时针旋转，使点A'落在AB边上．

(1)、求CA旋转到CA所构成的扇形的弧长．

(2)、判断BC与A'B'的位置关系．

查看试题解析