【提升卷】3.8圆内正多边形—北师大版数学九年级下册同步测试
试卷更新日期:2024-01-14 类型:同步测试
一、选择题
-
1. 一个圆的内接正六边形与内接正方形的边长之比为( )A、3:2 B、 C、 D、2. 如图,正五边形内接于 , 连接 , 则( )
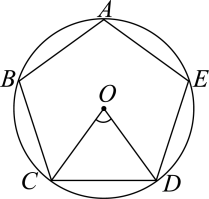 A、 B、 C、 D、3. 内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( ).A、 B、 C、3:2 D、1:24. 如图,正五边形内接于 , 点F在弧上.若 , 则的大小为( )
A、 B、 C、 D、3. 内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( ).A、 B、 C、3:2 D、1:24. 如图,正五边形内接于 , 点F在弧上.若 , 则的大小为( )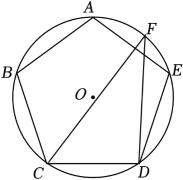 A、38° B、42° C、48° D、58°5. 如图,正九边形外接圆的半径是R,则这个正九边形的边长为( )
A、38° B、42° C、48° D、58°5. 如图,正九边形外接圆的半径是R,则这个正九边形的边长为( )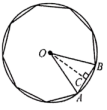 A、 B、 C、 D、6. 如图,正五边形内接于 , 点F是上的动点,则的度数为( )
A、 B、 C、 D、6. 如图,正五边形内接于 , 点F是上的动点,则的度数为( )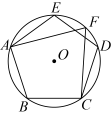 A、60° B、72° C、144° D、随着点的变化而变化7. 如图,正六边形和正方形都内接于 , 连接 , 则弦所对圆周角的度数为( )
A、60° B、72° C、144° D、随着点的变化而变化7. 如图,正六边形和正方形都内接于 , 连接 , 则弦所对圆周角的度数为( ) A、 B、 C、或 D、或8. 我们都知道蜂巢是很多个正六边形组合来的正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固、如图,某蜂巢的房孔是边长为的正六边形 , 若的内接正六边形为正六边形 , 则的长为( )
A、 B、 C、或 D、或8. 我们都知道蜂巢是很多个正六边形组合来的正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固、如图,某蜂巢的房孔是边长为的正六边形 , 若的内接正六边形为正六边形 , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,是矩形的外接圆,若 , 则图中阴影部分的面积为 . (结果保留)
 10. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正八边形的面积来近似估计的面积S,设的半径为2,则的值为 . (结果保留和根号)
10. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正八边形的面积来近似估计的面积S,设的半径为2,则的值为 . (结果保留和根号) 11. 据《汉书律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也”斛是中国古代的一种量器,“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为:正方形外接一个圆,此圆外是一个同心圆”.如图所示,现有一斛,其外圆直径为5尺(古代长度单位),两同心圆的外圆与内圆的半径之差为0.5尺,则此斛底面的正方形的边长为尺.
11. 据《汉书律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也”斛是中国古代的一种量器,“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为:正方形外接一个圆,此圆外是一个同心圆”.如图所示,现有一斛,其外圆直径为5尺(古代长度单位),两同心圆的外圆与内圆的半径之差为0.5尺,则此斛底面的正方形的边长为尺.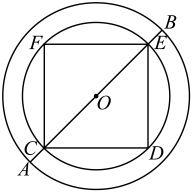 12. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM的度数是
12. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM的度数是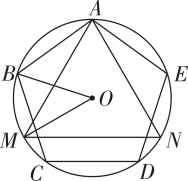 13. 如图是昆明西山的著名景点升庵亭,它的地基是半径为2m的正六边形,则该正六边形的边心距是 .
13. 如图是昆明西山的著名景点升庵亭,它的地基是半径为2m的正六边形,则该正六边形的边心距是 .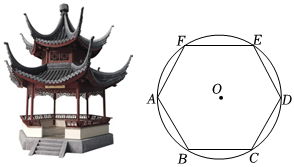
三、解答题
-
14. 尺规作图:如图,AD为⊙O的直径。
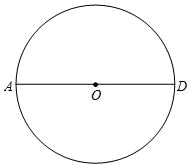 (1)、求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);(2)、已知连接DF,⊙O的半径为4,求DF的长。15. 如图,在正十二边形A1A2……A12 中,连结A3A7 , A7A10 , 求∠A3A7A10的度数.
(1)、求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);(2)、已知连接DF,⊙O的半径为4,求DF的长。15. 如图,在正十二边形A1A2……A12 中,连结A3A7 , A7A10 , 求∠A3A7A10的度数.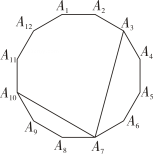 16. 如图,为正五边形的外接圆,已知 , 请用无刻度直尺完成下列作图,保留必要的画图痕迹.
16. 如图,为正五边形的外接圆,已知 , 请用无刻度直尺完成下列作图,保留必要的画图痕迹.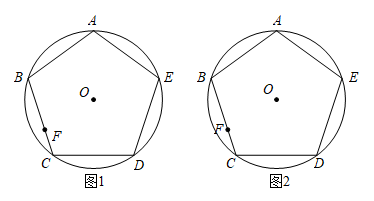 (1)、在图1中的边上求作点 , 使;(2)、在图2中的边上求作点 , 使 .17. 图1是某景区的纪念币,一面有一个正十边形,示意图如图2所示,其外接圆的圆心为O,直径为 .
(1)、在图1中的边上求作点 , 使;(2)、在图2中的边上求作点 , 使 .17. 图1是某景区的纪念币,一面有一个正十边形,示意图如图2所示,其外接圆的圆心为O,直径为 .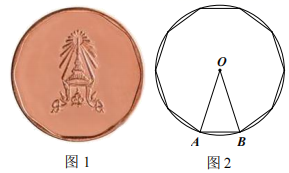 (1)、求这个正十边形的边长 .(2)、求这个正十边形的面积.(参考数据: )18. 如图甲所示,正五边形ABCDE内接于⊙O,阅读以下作图过程,并回答相关问题:
(1)、求这个正十边形的边长 .(2)、求这个正十边形的面积.(参考数据: )18. 如图甲所示,正五边形ABCDE内接于⊙O,阅读以下作图过程,并回答相关问题:作法如图乙所示.①作直径AF.②以F为圆心,FO为半径作圆弧,与⊙O交于点M,N.③连结AM,MN,NA.
 (1)、求∠ABC的度数.(2)、△AMN是正三角形吗?请说明理由.(3)、从点A开始,以DN长为半径,在⊙O上依次截取点,再依次连结这些分点,得到正n边形,求n的值.19. 如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)、求∠ABC的度数.(2)、△AMN是正三角形吗?请说明理由.(3)、从点A开始,以DN长为半径,在⊙O上依次截取点,再依次连结这些分点,得到正n边形,求n的值.19. 如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON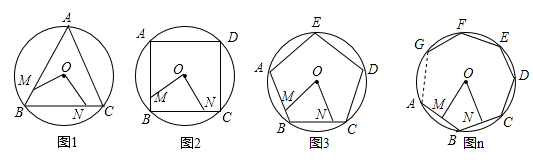 (1)、求图1中∠MON的度数(2)、图2中∠MON的度数是 , 图3中∠MON的度数是(3)、试探究∠MON的度数与正n边形边数n的关系是
(1)、求图1中∠MON的度数(2)、图2中∠MON的度数是 , 图3中∠MON的度数是(3)、试探究∠MON的度数与正n边形边数n的关系是