【培优卷】3.8圆内正多边形—北师大版数学九年级下册同步测试
试卷更新日期:2024-01-14 类型:同步测试
一、选择题
-
1. 如图,在圆内接正六边形ABCDEF中,BF , BD分别交AC于点G , H , 若该圆的半径为12,则线段GH的长为( )
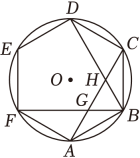 A、6 B、 C、 D、82. 如图,正方形和等边三角形均内接于 , 则的值为( )
A、6 B、 C、 D、82. 如图,正方形和等边三角形均内接于 , 则的值为( )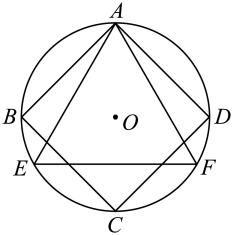 A、 B、 C、 D、3. 如图,等边△ABC是⊙O的内接三角形,点D,E分别为AB,AC边上的中点,延长DE交⊙O于点F,若BC=2,则EF=( )
A、 B、 C、 D、3. 如图,等边△ABC是⊙O的内接三角形,点D,E分别为AB,AC边上的中点,延长DE交⊙O于点F,若BC=2,则EF=( )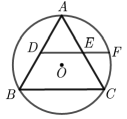 A、 B、 C、 D、4. 如图,点是的六等分点.若 , 的周长分别为 , , 面积分别为 , , 则下列正确的是( )
A、 B、 C、 D、4. 如图,点是的六等分点.若 , 的周长分别为 , , 面积分别为 , , 则下列正确的是( )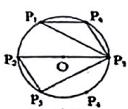 A、 B、 C、 D、5. 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( ).
A、 B、 C、 D、5. 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( ).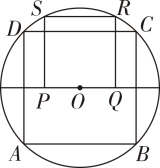 A、1 :2 B、1:3 C、2:3 D、2:56. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A、1 :2 B、1:3 C、2:3 D、2:56. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )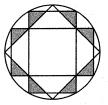 A、1 B、 C、 D、7. ⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )A、1∶ B、 ∶ C、3∶2 D、1∶28. 小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他制了如图2所示的图形,图2中六个形状大小都相同的四边形围成一个圆的内接六边和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为 , 则该圆的半径为( )cm.
A、1 B、 C、 D、7. ⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )A、1∶ B、 ∶ C、3∶2 D、1∶28. 小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他制了如图2所示的图形,图2中六个形状大小都相同的四边形围成一个圆的内接六边和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为 , 则该圆的半径为( )cm.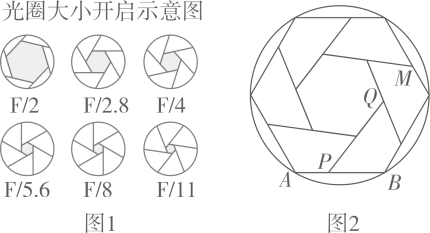 A、 B、 C、7 D、8
A、 B、 C、7 D、8二、填空题
-
9. 请阅读下列材料,解答问题:
克罗狄斯托勒密约年年 , 是希腊数学家,天文学家,地理学家和占星家.在数学方面,他还论证了四边形的特性,即有名的托勒密定理.
托勒密定理:圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.
如图,正五边形内接于 , , 则对角线的长为 .
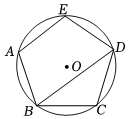 10. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .
10. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .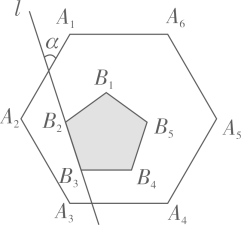 11. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率.若设⊙O的半径为R , 圆内接正n边形的边长、面积分别为an , Sn , 圆内接正2n边形边长、面积分别为a2n , S2n . 刘徽用以下公式求出a2n和S2n . , .如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 .
11. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率.若设⊙O的半径为R , 圆内接正n边形的边长、面积分别为an , Sn , 圆内接正2n边形边长、面积分别为a2n , S2n . 刘徽用以下公式求出a2n和S2n . , .如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 . 12. 拓展课上,同学们准备用卡纸做一个底面为边长为的正六边形,高为的无盖包装盒,它的表面展开图如图1所示.
12. 拓展课上,同学们准备用卡纸做一个底面为边长为的正六边形,高为的无盖包装盒,它的表面展开图如图1所示.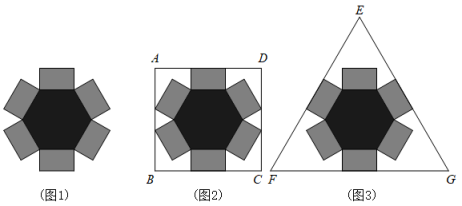 (1)、若选用长方形卡纸按图2方式剪出包装盒的表面展开图,则的长为;(2)、若选用一块等边三角形卡纸按图3方式剪出包装盒表面展开图,则这个等边三角形的边长为.
(1)、若选用长方形卡纸按图2方式剪出包装盒的表面展开图,则的长为;(2)、若选用一块等边三角形卡纸按图3方式剪出包装盒表面展开图,则这个等边三角形的边长为.三、实践探究题
-
13. 某数学学习小组的成员在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行了如下探讨:
甲同学:我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学:但是边数为3时,它是正三角形,而且我猜想,边数为5时,它应该是正五边形……
丙同学:我发现边数为6时,它也不一定是正六边形.如图甲所示,是正三角形,均相等,很显然由此构造的六边形ADBECF并不是正六边形.
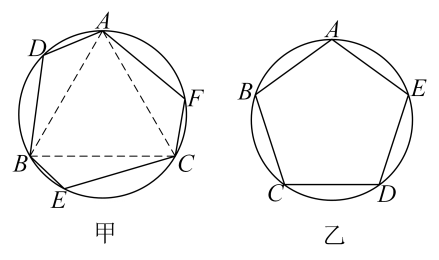 (1)、如图乙所示,若圆内接五边形ABCDE的各内角均相等,则∠ABC= .请简要说明圆内接五边形ABCDE为正五边形的理由.(2)、请证明丙同学构造的六边形各内角相等.(3)、根据以上的探索过程,就“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,请提出你的猜想.(不需证明)14. 如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.
(1)、如图乙所示,若圆内接五边形ABCDE的各内角均相等,则∠ABC= .请简要说明圆内接五边形ABCDE为正五边形的理由.(2)、请证明丙同学构造的六边形各内角相等.(3)、根据以上的探索过程,就“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,请提出你的猜想.(不需证明)14. 如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.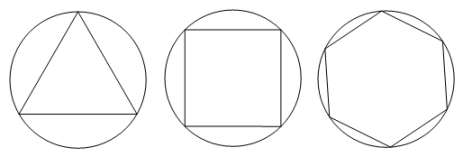 (1)、角的“接近度”定义:设正n边形的每个内角的度数为 , 将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,
(1)、角的“接近度”定义:设正n边形的每个内角的度数为 , 将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,①若 , 则该正n边形的“接近度”等于.
②若 , 则该正n边形的“接近度”等于.
③当“接近度”等于.时,正n边形就成了圆.
(2)、边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为.分别计算时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?15. 阅读下列材料,并按要求完成相应的任务.黄金三角形与五角星
当等腰三角形的顶角为36°(或108°)时,它的底与腰的比(或腰与底的比)为 , 我们把这样的三角形叫做黄金三角形.
按下面的步骤画一个五角星(如图):
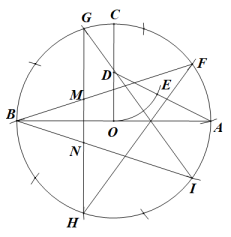
①作一个以AB为直径的圆,圆心为O;
②过圆心O作半径OC⊥AB;
③取OC的中点D,连接AD;
④以D为圆心OD为半径画弧交AD于点E;
⑤从点A开始以AE为半径顺时针依次画弧,
正好把⊙O十等分(其中点F,G,B,H,I为五等分点);
⑥以点F,G,B,H,I为顶点画出五角星.
任务:
(1)、求出的值为;(2)、如图,GH与BF,BI分别交于点M,N,求证:△BMN是黄金三角形.