【提升卷】3.7切线长定理—北师大版数学九年级下册同步测试
试卷更新日期:2024-01-14 类型:同步测试
一、选择题
-
1. 如图,分别与相切于A、B两点,连接 , 若 , 则的度数为( )
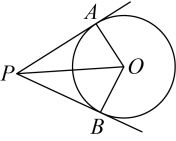 A、 B、 C、 D、2. 根钢管放在V形架内,如图是其截面图,O为钢管的圆心,如果钢管的直径为20cm,∠MPN=60°,则OP的长度是( )
A、 B、 C、 D、2. 根钢管放在V形架内,如图是其截面图,O为钢管的圆心,如果钢管的直径为20cm,∠MPN=60°,则OP的长度是( ) A、40cm B、40cm C、20cm D、20cm3. 如图,已知半圆O与四边形的边相切,切点分别为D,E,C,设半圆的半径为2, , 则四边形的周长为( )
A、40cm B、40cm C、20cm D、20cm3. 如图,已知半圆O与四边形的边相切,切点分别为D,E,C,设半圆的半径为2, , 则四边形的周长为( ) A、7 B、9 C、12 D、144. 如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )
A、7 B、9 C、12 D、144. 如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )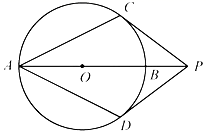 A、 B、 C、 D、5. 如图, 、 分别与 相切于 、 , , 为 上一点,则 的度数为( )
A、 B、 C、 D、5. 如图, 、 分别与 相切于 、 , , 为 上一点,则 的度数为( )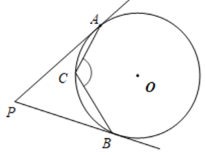 A、 B、 C、 D、6. 如图, 切 于点 切 于点 交 于点 ,下列结论中不一定成立的是( )
A、 B、 C、 D、6. 如图, 切 于点 切 于点 交 于点 ,下列结论中不一定成立的是( )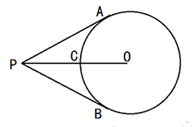 A、 B、 平分 C、 D、7. 如图, 是 的直径,点 在 的延长线上, , 与 相切于点 , 交 的延长线于点 ,若 的半径为2,则 的长是( )
A、 B、 平分 C、 D、7. 如图, 是 的直径,点 在 的延长线上, , 与 相切于点 , 交 的延长线于点 ,若 的半径为2,则 的长是( ) A、4 B、 C、 D、38. 探究性学习小组的同学接受了测量同样型号圆柱工件直径的任务.他们使用的工具是有一个角是60°的直角三角板和刻度尺.小明的测量方法如图甲所示.测得PC=12cm.小亮的测量方法如图乙所示.则与QA的值最接近的是( )
A、4 B、 C、 D、38. 探究性学习小组的同学接受了测量同样型号圆柱工件直径的任务.他们使用的工具是有一个角是60°的直角三角板和刻度尺.小明的测量方法如图甲所示.测得PC=12cm.小亮的测量方法如图乙所示.则与QA的值最接近的是( ) A、8cm B、7 cm C、6 cm D、5 cm
A、8cm B、7 cm C、6 cm D、5 cm二、填空题
-
9. 如图,在中, , , 为的中点,分别与 , 相切于 , 两点,则的半径长为 .
 10. 将一把直尺,一块含有的直角三角板和一张光盘如图摆放,已知点A为三角板角与直尺的交点,点B为直尺与光盘的交点, , 则光盘直径是.
10. 将一把直尺,一块含有的直角三角板和一张光盘如图摆放,已知点A为三角板角与直尺的交点,点B为直尺与光盘的交点, , 则光盘直径是. 11. 如图,正方形ABCD的边长为4,点E是CD边上一点,连接AE,过点B作BG⊥AE于点G,连接CG并延长交AD于点F,则AF的最大值是 .
11. 如图,正方形ABCD的边长为4,点E是CD边上一点,连接AE,过点B作BG⊥AE于点G,连接CG并延长交AD于点F,则AF的最大值是 . 12. 如图,是一个小型花园,阴影部分为一个圆形水池,且与三边相切,已知 , , , 若从天空飘落下一片树叶恰好落入花园里,则落入水池的概率(取).
12. 如图,是一个小型花园,阴影部分为一个圆形水池,且与三边相切,已知 , , , 若从天空飘落下一片树叶恰好落入花园里,则落入水池的概率(取). 13. 如图,半径为 的⊙O与边长为8的等边三角形ABC的两边AB、BC都相切,连接OC,则sin∠OCB=.
13. 如图,半径为 的⊙O与边长为8的等边三角形ABC的两边AB、BC都相切,连接OC,则sin∠OCB=.
三、作图题
-
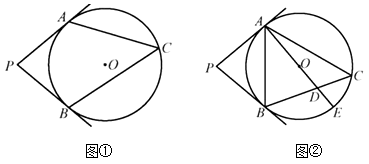
14. 如图,PA,PB是圆的切线,A,B为切点.
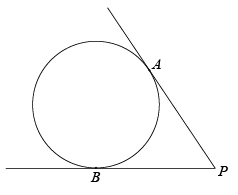 (1)、求作:这个圆的圆心O(用尺规作图,保留作图痕迹,不写作法和证明);(2)、在(1)的条件下,延长AO交射线PB于C点,若AC=4,PA=3,请补全图形,并求⊙O的半径.
(1)、求作:这个圆的圆心O(用尺规作图,保留作图痕迹,不写作法和证明);(2)、在(1)的条件下,延长AO交射线PB于C点,若AC=4,PA=3,请补全图形,并求⊙O的半径.四、解答题
-
15. 如图1,一个圆球放置在V型架中.图2是它的平面示意图,CA、CB都是⊙O的切线,切点分别是A、B,如果⊙O的半径为 cm,且AB=6cm,求∠ACB.
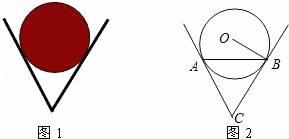
-