【培优卷】3.7切线长定理—2023-2024学年北师大版九年级下册同步测试

试卷更新日期：2024-01-14 类型：同步测试

进入出卷网下载

一、选择题

1. 如图， $△ A B C$ 的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，已知 $△ A B C$ 的周长为36． $A B = 9$ ， $B C = 14$ ，则AF的长为（）

A、4 B、5 C、9 D、13

查看试题解析
2. 如图PA、PB分别与⊙O相切于A．B两点，点C为⊙O上一点，连接AC．BC，若∠ACB=60°，则 $∠ P$ 的度数为（）

A、60° B、65° C、 $50 °$ D、 $55 °$

查看试题解析
3. 如图，PA、PB、MN是⊙O的切线，A、B、C是切点，MN分别交线段PA、PB于M、N两点.若∠APB＝50°，则∠MON＝（）

A、50° B、60° C、65° D、70°

查看试题解析
4. 如图，从圆外一点P引圆的两条切线PA，PB，A，B为切点，C为PB上的一点，连接CO交⊙O于点D，若 $C D ∥ P A$ ， $P A = 9$ ， $C D = 2$ ，则⊙O的半径长是（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、4 D、3

查看试题解析
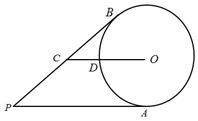5. 如图， $P A$ 、 $P B$ 为⊙O的切线，切点分别为A、B， $P O$ 交 $A B$ 于点C， $P O$ 的延长线交⊙O于点D．下列结论不一定成立的是（）

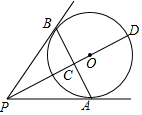A、 $△ B P A$ 为等腰三角形 B、 $A B$ 与 $P D$ 相互垂直平分 C、点A，B都在以 $P O$ 为直径的圆上 D、 $P C$ 为 $△ B P A$ 的边 $A B$ 上的中线

查看试题解析
6. 已知PA ， PB是⊙O的切线，A ， B是切点，点C是⊙O上不同于点A、点B的一个动点，若∠P＝54°，则∠ACB的度数是（　　）

A、63° B、117° C、53°或127° D、117°或63°

查看试题解析
7. 如图，在△AOB中，∠AOB＝90°，OB＝3，半径为1的⊙O与OB交于点C，且AB与⊙O相切，过点C作CD⊥OB交AB于点D，点M是边OA上动点．则△MCD周长最小值为（　　）

A、2 $\sqrt{2}$ B、 $\frac{\sqrt{6} + \sqrt{2}}{2}$ C、 $\sqrt{2}$ + $\frac{5}{3}$ D、 $\frac{5 \sqrt{2}}{3}$

查看试题解析
8. 如图，在矩形ABCD中，点E在CD边上，连接AE，将 $△ A D E$ 沿AE翻折，使点D落在BC边的点F处，连接AF，在AF上取点O，以O为圆心，线段OF的长为半径作⊙O，⊙O与AB，AE分别相切于点G，H，连接FG，GH.则下列结论错误的是（）

A、 $∠ B A E = 2 ∠ D A E$ B、四边形EFGH是菱形 C、 $A D = 3 C E$ D、 $G H ⊥ A O$

查看试题解析

二、填空题

9. 如图所示，过半径为6cm的⊙O外一点P引圆的切线PA，PB，连接PO交⊙O于F，过F作⊙O的切线，交PA，PB分别于D，E，如果PO=10cm，∠APB=40°，则△PED的周长=；∠DOE的度数=

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 6$ ， $B C = 2 \sqrt{3}$ ，半径为1的 $⊙ O$ 在 $R t △ A B C$ 内平移（ $⊙ O$ 可以与该三角形的边相切），则点 $A$ 到 $⊙ O$ 上的点的距离的最大值为.

查看试题解析
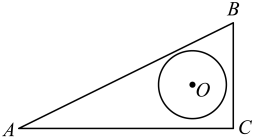11. 如图，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过△ABC的内切圆圆心O，且点E在半圆弧上．若正方形DEFG的面积为100，且△ABC的内切圆半径r=4，则半圆的直径AB= ．

查看试题解析
12. 如图，△ABC是一块直角三角板，且∠C＝90°，∠A＝30°，现将圆心为点O的圆形纸片放置在三角板内部，将圆形纸片沿着三角板的内部边缘滚动1周，回到起点位置时停止，若BC＝7+2 $\sqrt{3}$ ，圆形纸片的半径为2，求圆心O运动的路径长为．

查看试题解析

三、综合题

13. 如图，以矩形ABCD的边CD为直径作 $⊙ O$ ，点E是AB的中点，连接CE交 $⊙ O$ 于点F，连接AF并延长交BC于点H．

(1)、若连接AO，试判断四边形AECO的形状，并说明理由；

(2)、求证：AH是 $⊙ O$ 的切线；

(3)、若 $A B = 6$ ， $C H = 2$ ，求AH的长．

查看试题解析
14. 如图，AB是 $⊙ O$ 的直径，PA，PC是 $⊙ O$ 的两条切线，点A，C为切点，延长PC，AB相交于点D，若BD＝1，CD＝3，点F为弧AB的中点，连接AC．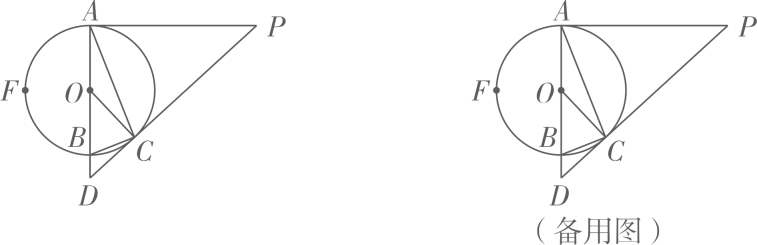

(1)、连接OP交AC于点M，求证： $∠ A C B = ∠ A M O$ ；

(2)、设 $∠ O C B = α$ ，求 $\tan α$ 的值；

(3)、若点G与点F关于圆心O对称，连接CG，求CG的长．

查看试题解析
15. 我们给出以下定义：如图（1）若点P在不大于 $90 °$ 的 $∠ M O N$ 的内部，作 $P Q ⊥ O M$ 于点Q， $P I ⊥ O N$ 于点I，则 $P Q + P I$ 称为点P与 $∠ M O N$ 的“点角距离”记作 $d (P ， ∠ M O N)$ .如图（2）在平面直角坐标系 $x o y$ 中，x、y的正半轴组成的 $∠ X O Y$ ， O为坐标原点.

(1)、如图（2）点 $A (4 ， 1)$ ，则 $d (A ， ∠ X O Y) =$ ；

(2)、若点B为 $∠ X O Y$ 内一点， $d (B ， ∠ X O Y) = 6$ ，以点B为圆心r为半径作圆， $⊙ B$ 与x轴、y轴均相切，求点B的坐标；

(3)、已知点 $C (2 ， 4)$ .
①已知点D的坐标为 $(1 ， 3)$ ，求 $O C$ 的解析式和 $d (D ， ∠ C O Y)$ 的值.
②已知点 $E (s ， t)$ 在 $∠ C O Y$ 的内部， $d (E ， ∠ C O Y) = \frac{2 \sqrt{5}}{5} t - \frac{3 \sqrt{5}}{5} s$ ，当s为大于0的任意实数时，代数式 $m t - \sqrt{5} s - m s + 3 m$ （m为常数）的值为定值，求m的值及该定值.

查看试题解析