【基础卷】3.7切线长定理—北师大版数学九年级下册同步测试
试卷更新日期:2024-01-14 类型:同步测试
一、选择题
-
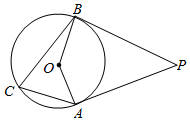
1. 如图,PA、PB分别切⊙O于A,B,∠APB=60°,⊙O半径为2,则PB的长为( )
 A、3 B、4 C、 D、2. PA、PB分别切⊙O于A、B两点,C为⊙O上一动点(点C不与A、B重合),∠APB=50°,则∠ACB=( )A、100° B、115° C、65°或115° D、65°3. 如图,⊙O与正方形ABCD的两边AB,AD相切,且DE与⊙O相切于E点.若⊙O的半径为4,且AB=10,则DE的长度为( )
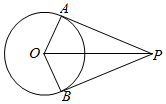
A、3 B、4 C、 D、2. PA、PB分别切⊙O于A、B两点,C为⊙O上一动点(点C不与A、B重合),∠APB=50°,则∠ACB=( )A、100° B、115° C、65°或115° D、65°3. 如图,⊙O与正方形ABCD的两边AB,AD相切,且DE与⊙O相切于E点.若⊙O的半径为4,且AB=10,则DE的长度为( ) A、5 B、6 C、 D、4. 如图,已知和分别是的切线,A、B是切点,连接 , 已知 , 则的度数是( )
A、5 B、6 C、 D、4. 如图,已知和分别是的切线,A、B是切点,连接 , 已知 , 则的度数是( ) A、 B、 C、 D、5. 如图,PA、PB是⊙O的两条切线,切点分别是A、B,且∠APB=60°,⊙O的半径为3,则阴影部分的面积为( )
A、 B、 C、 D、5. 如图,PA、PB是⊙O的两条切线,切点分别是A、B,且∠APB=60°,⊙O的半径为3,则阴影部分的面积为( )
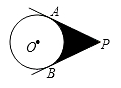 A、 B、 C、18-6π D、18-3π6. 如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,点D是劣弧上的一点,则∠ADB=( )
A、 B、 C、18-6π D、18-3π6. 如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,点D是劣弧上的一点,则∠ADB=( )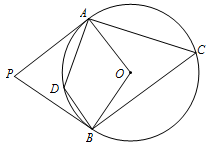 A、108° B、72° C、54° D、126°7. 如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,若∠DEF=52°,则∠A的度数是( )
A、108° B、72° C、54° D、126°7. 如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,若∠DEF=52°,则∠A的度数是( )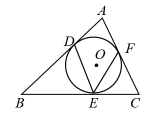 A、52° B、76° C、26° D、128°8. 如图, 、 、 是 的切线,切点分别为P、C、D,若 , ,则 的长是( )
A、52° B、76° C、26° D、128°8. 如图, 、 、 是 的切线,切点分别为P、C、D,若 , ,则 的长是( )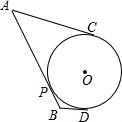 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
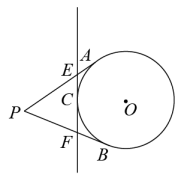
9. 如图,PA、PB分别与⊙O相切于点A、B,直线EF与⊙O相切于点C,分别交PA、PB于E、F,且PA=8cm,则△PEF的周长为 cm.
 10. 如图,在△ABC中,AC=BC , ∠ACB=100°,⊙O与AB , BC分别切于点D , C , 连接CD . 则∠ACD的度数为 .
10. 如图,在△ABC中,AC=BC , ∠ACB=100°,⊙O与AB , BC分别切于点D , C , 连接CD . 则∠ACD的度数为 . 11. 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,则∠P=度.
11. 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,则∠P=度. 12. 如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为 .
12. 如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为 .
三、解答题