【提升卷】3.6直线与圆的位置关系—北师大版数学九年级下册同步测试
试卷更新日期:2024-01-14 类型:同步测试
一、选择题
-
1. 在平面直角坐标系中,以点为圆心,为半径作 , 下列判断正确的是( )A、与轴相交 B、与轴相切 C、点在外 D、点在内2. 如图,已知△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E.若CD=5,CE=4,则⊙O的半径是( )
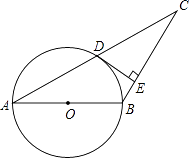 A、3 B、4 C、 D、3. 如图,是的直径,与相切于点 , , 的延长线交于点 , 则的度数是( )
A、3 B、4 C、 D、3. 如图,是的直径,与相切于点 , , 的延长线交于点 , 则的度数是( ) A、 B、 C、 D、4. 如图,是的直径,是的切线,连接交于点 , 连接 , , , 则的长为( )
A、 B、 C、 D、4. 如图,是的直径,是的切线,连接交于点 , 连接 , , , 则的长为( ) A、
A、
B、
C、
D、5. 如图,是的直径,为上一点,垂直平分交于点 , 过点的切线与的延长线交于点若 , 则的长为( ) A、 B、 C、 D、6. 如图,以的边为直径的恰好过的中点 , 过点作于 , 连接 , 则下列结论中:;;; , 其中一定正确的结论有( )
A、 B、 C、 D、6. 如图,以的边为直径的恰好过的中点 , 过点作于 , 连接 , 则下列结论中:;;; , 其中一定正确的结论有( )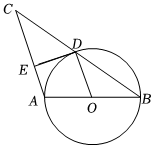 A、1个 B、2个 C、3个 D、4个7. 如图,已知中, , . D、E分别是边、上的点, , 且 . 如果经过点A,且与外切,那么与直线的位置关系是( )
A、1个 B、2个 C、3个 D、4个7. 如图,已知中, , . D、E分别是边、上的点, , 且 . 如果经过点A,且与外切,那么与直线的位置关系是( ) A、相离 B、相切 C、相交 D、不能确定8. 在中, , 以点C为圆心,R为半径作圆.若与边只有一个公共点,则R的取值范围是( )A、 B、 C、或 D、或
A、相离 B、相切 C、相交 D、不能确定8. 在中, , 以点C为圆心,R为半径作圆.若与边只有一个公共点,则R的取值范围是( )A、 B、 C、或 D、或二、填空题
-
9. 如图,分别与相切于两点,且 . 若点是上异于点的一点,则的大小为 .
 10. 如图,已知 的半径为2,圆心P在抛物线 上运动;当 与x轴相切时;圆心P的坐标为.
10. 如图,已知 的半径为2,圆心P在抛物线 上运动;当 与x轴相切时;圆心P的坐标为.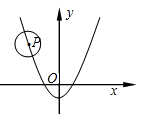 11. 如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD分别与⊙O相切于点C,D,若∠CPA=40°,则∠CAD的度数为°.
11. 如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD分别与⊙O相切于点C,D,若∠CPA=40°,则∠CAD的度数为°.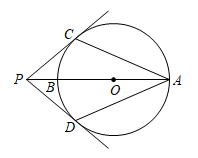 12. 在数学课上,老师请同学思考如下问题:
12. 在数学课上,老师请同学思考如下问题:已知:在ABC中,∠A=90°.

求作:⊙P,使得点P在边AC上,且⊙P与AB,BC都相切.
嘉淇的主要作法如下:
如图,

⑴作∠ABC的平分线BF,与AC交于点P;
⑵以点P为圆心,AP长为半径作⊙P.所以⊙P即为所求.
老师说:“嘉淇的作法符合题意.”请回答:⊙P与BC相切的依据是①;② .
三、解答题
-
13. 如图,AB为⊙O的切线,B为切点,过点B作BC⊥OA , 垂足为点E , 交⊙O于点C , 连接CO并延长CO与AB的延长线交于点D , 连接AC .
 (1)、求证:AC为⊙O的切线;(2)、若⊙O半径为3,OD=5.求线段AD的长.
(1)、求证:AC为⊙O的切线;(2)、若⊙O半径为3,OD=5.求线段AD的长.

