【培优卷】3.6直线与圆的位置关系—北师大版数学九年级下册同步测试
试卷更新日期:2024-01-14 类型:同步测试
一、选择题
-
1. 如图,正方形 的顶点A、D在⊙O上,边 与⊙O相切,若正方形 的周长记为 ,⊙O的周长记为 ,则 、 的大小关系为( )
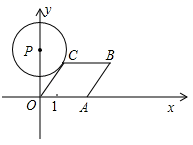
 A、 B、 C、 D、无法判断2. 如图,直线y= x+ 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
A、 B、 C、 D、无法判断2. 如图,直线y= x+ 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( ) A、3 B、4 C、5 D、63. 如图,△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,点E是线段AD上一点,以点E为圆心,r为半径作⊙E.若⊙E与边AB,AC相切,而与边BC相交,则半径r的取值范围是( )
A、3 B、4 C、5 D、63. 如图,△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,点E是线段AD上一点,以点E为圆心,r为半径作⊙E.若⊙E与边AB,AC相切,而与边BC相交,则半径r的取值范围是( ) A、r> B、 <r≤4 C、 <r≤4 D、 <r≤4. 以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )A、0≤b<2 B、﹣2 C、﹣2 2 D、﹣2 <b<25. 矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )
A、r> B、 <r≤4 C、 <r≤4 D、 <r≤4. 以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )A、0≤b<2 B、﹣2 C、﹣2 2 D、﹣2 <b<25. 矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )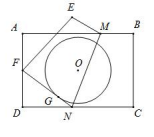 A、3.6 B、 C、3.5 D、6. 如图,在平面直角坐标系中,动点A、B分别在x轴上和函数y=x的图象上,AB=4,CB⊥AB,BC=2,则OC的最大值为( )
A、3.6 B、 C、3.5 D、6. 如图,在平面直角坐标系中,动点A、B分别在x轴上和函数y=x的图象上,AB=4,CB⊥AB,BC=2,则OC的最大值为( )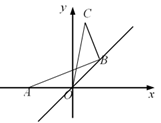 A、2 +2 B、2 +4 C、2 D、2 +27. 如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,CP的长为( )
A、2 +2 B、2 +4 C、2 D、2 +27. 如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,CP的长为( )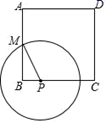 A、3或 B、3或 C、5或 D、5或8. 如图,Rt△ACB中,∠C=90°,AC=6,BC=8,半径为1的⊙O与AC,BC相切,当⊙O沿边CB平移至与AB相切时,则⊙O平移的距离为( )
A、3或 B、3或 C、5或 D、5或8. 如图,Rt△ACB中,∠C=90°,AC=6,BC=8,半径为1的⊙O与AC,BC相切,当⊙O沿边CB平移至与AB相切时,则⊙O平移的距离为( )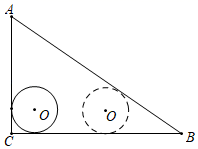 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
9. 如图,已知A点从点出发,以每秒1个单位长度的速度沿着x轴的正方向运动,经过t秒后,以O,A为顶点作菱形 , 使B,C点都在第一象限内,且 , 若以为圆心,为半径的圆恰好与所在的直线相切,则.
 10. 已知矩形OABC中,O为坐标原点,点A在x轴上,点C在y轴上,B的坐标为(10,5),点P在边BC上,点A关于OP的对称点为A',若点A'到直线BC的距离为4,则点A'的坐标可能为 .11. 如图,点P在函数的图象上运动,O为坐标原点,点A为的中点,以点P为圆心,为半径作 , 则当与坐标轴相切时,点P的坐标为 .
10. 已知矩形OABC中,O为坐标原点,点A在x轴上,点C在y轴上,B的坐标为(10,5),点P在边BC上,点A关于OP的对称点为A',若点A'到直线BC的距离为4,则点A'的坐标可能为 .11. 如图,点P在函数的图象上运动,O为坐标原点,点A为的中点,以点P为圆心,为半径作 , 则当与坐标轴相切时,点P的坐标为 . 12. 已知正方形ABCD中,AB=2,⊙A是以A为圆心,1为半径的圆,若⊙A绕点B顺时针旋转,旋转角为α(0°<α<180°),则当旋转后的圆与正方形ABCD的边相切时,α= .
12. 已知正方形ABCD中,AB=2,⊙A是以A为圆心,1为半径的圆,若⊙A绕点B顺时针旋转,旋转角为α(0°<α<180°),则当旋转后的圆与正方形ABCD的边相切时,α= .三、综合题
-
13. 平面直角坐标系xOy中,点A(x1 , y1)与B(x2 , y2),如果满足x1+x2=0,y1﹣y2=0,其中x1≠x2 , 则称点A与点B互为反等点.已知:点C(3,4)
 (1)、下列各点中,点C互为反等点;
(1)、下列各点中,点C互为反等点;D(﹣3,﹣4),E(3,4),F(﹣3,4)
(2)、已知点G(﹣5,4),连接线段CG,若在线段CG上存在两点P,Q互为反等点,求点P的横坐标xP的取值范围;(3)、已知⊙O的半径为r,若⊙O与(2)中线段CG的两个交点互为反等点,求r的取值范围.14. 如图,二次函数的图像与轴分别交于点(点A在点的左侧),直线是对称轴.点在函数图象上,其横坐标大于4,连接 , 过点作 , 垂足为 , 以点为圆心,作半径为的圆,与相切,切点为 .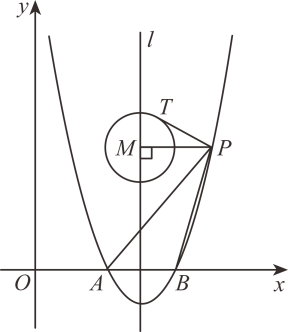 (1)、求点的坐标;(2)、若以的切线长为边长的正方形的面积与的面积相等,且不经过点 , 求长的取值范围.15.
(1)、求点的坐标;(2)、若以的切线长为边长的正方形的面积与的面积相等,且不经过点 , 求长的取值范围.15. (1)、如图 , 在中, , , 若的半径为 , 点在上,点在上,连接 , 求线段的最小值;(2)、如图所示,五边形是某市工业新区的外环路,新区管委会在点处,点处是该市的一个交通枢纽已知: , , 根据新区的自然环境及实际需求,现要在矩形区域内含边界修一个半径为的圆型环道;过圆心 , 作 , 垂足为 , 与交于点连接 , 点在上,连接其中,线段、及是要修的三条道路,要在所修迅路、之和最短的情况下,使所修道路最短,试求此时环道的圆心到的距离的长.
(1)、如图 , 在中, , , 若的半径为 , 点在上,点在上,连接 , 求线段的最小值;(2)、如图所示,五边形是某市工业新区的外环路,新区管委会在点处,点处是该市的一个交通枢纽已知: , , 根据新区的自然环境及实际需求,现要在矩形区域内含边界修一个半径为的圆型环道;过圆心 , 作 , 垂足为 , 与交于点连接 , 点在上,连接其中,线段、及是要修的三条道路,要在所修迅路、之和最短的情况下,使所修道路最短,试求此时环道的圆心到的距离的长.