【培优卷】3.5确定圆的条件—2023-2024学年北师大版九年级下册同步测试

试卷更新日期：2024-01-14 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，方格纸上每个小正方形的边长均为1个单位长度，点O，A，B，C均在格点（两条网格线的交点叫格点）上，以点O为原点建立平面直角直角坐标系，则过A，B，C三点的圆的圆心坐标为（）

A、 $(- 1 ， - 1)$ B、 $(- 2 ， - 1)$ C、 $(- 1 ， - 2)$ D、 $(- 2 ， - 2)$

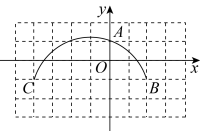查看试题解析
2. 在平面直角坐标系中，已知点A（0，1），B（0，﹣5），若在x轴正半轴上有一点C，使∠ACB＝30°，则点C的横坐标是（）

A、3 $\sqrt{3} +$ 4 $\sqrt{2}$ B、12 C、6+3 $\sqrt{3}$ D、6 $\sqrt{3}$

查看试题解析
3. 如图，在 $5 \times 5$ 的正方形网格中（小正方形的连长为1），有6个点A、B、C、D、E、F，若过A、B、C三点作圆O，则点D、E、F三点中在圆O外的有（）个

A、0 B、1 C、2 D、3

查看试题解析
4. 如图，在平面直角坐标系中，O为坐标原点， $Δ A O B$ 为 $R t Δ$ ，点A的坐标是 $(1 ， 0)$ ， $∠ B A O = 60 °$ ，把 $R t Δ A O B$ 绕点A按顺时针方向旋转 $90 °$ 后，得到 $R t Δ A O^{'} B^{'}$ ，则 $R t Δ A O^{'} B^{'}$ 的外接圆圆心坐标是（）

A、 $(1 + \frac{\sqrt{3}}{2} ， \frac{1}{2})$ B、 $(\frac{\sqrt{3}}{2} ， \frac{1}{2})$ C、 $(\frac{1 + \sqrt{3}}{2} ， 1)$ D、 $(\frac{1}{2} ， \frac{1 + \sqrt{3}}{2})$

查看试题解析
5. 如图，已知△ABC内接于半径为1的⊙O，∠BAC=θ（θ是锐角），则△ABC的面积的最大值为（）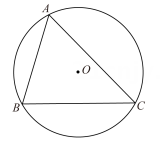

A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)

查看试题解析
6. 如图，AB＝AD＝6，∠A＝60°，点C在∠DAB内部且∠C＝120°，则CB＋CD的最大值（）

A、4 $\sqrt{3}$ B、8 C、10 D、6 $\sqrt{3}$

查看试题解析
7. 图，抛物线 $y = \frac{1}{2} x^{2} - \frac{1}{2} x - 3$ 的图像与x轴交于点A，B，交y轴于点C，动点P在射线AB运动，作△BCP的外接圆⊙M，当圆心M落在该抛物线上时，则AP的值（）

A、3 B、4 C、5 D、3.5

查看试题解析
8. 如图，以点 $O$ 为圆心， $4$ 为半径作扇形 $A O B ，$ 已知： $A O ⊥ B O ，$ 点 $E$ 在 $O A$ 上，且 $0 E = 2 \sqrt{3} ， C D$ 垂直平分 $O B ，$ 动点 $P$ 在线段 $C D$ 上运动(不与点 $D$ 重合)，设 $△ O D P$ 的外心为 $I$ ，则 $E I$ 的最小值为（）

A、 $1$ B、 $2$ C、 $2 \sqrt{3} - 1$ D、 $\sqrt{3} + 1$

查看试题解析

二、填空题

9. 如图，点B、E、C在一直线上， $△ B E A ， △ C E D$ 在直线 $B C$ 同侧， $B E = B A = 2 ， C E = C D = 3$ ， $∠ B = ∠ C = α$ ，当 $\tan \frac{α}{2} = \frac{1}{2}$ 时， $△ A D E$ 外接圆的半径为．

查看试题解析
10. 一个直角三角形的两条边长是方程x²﹣7x+12＝0的两个根，则此直角三角形的外接圆的直径为.

查看试题解析
11. 如图，在 $△ A B C$ 中， $∠ A C B = 30^{\circ} ， D$ 为 $B A$ 延长线上一点，连接 $C D ， ∠ D = 60^{\circ}$ ，则 $\frac{A D}{A B}$ 的最大值是．

查看试题解析
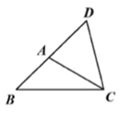12. 如图， $△ A B C$ 和 $△ C D E$ 都是等边三角形， $A B > C D$ ， $A B = 6$ ，固定 $△ A B C$ ，把 $△ C D E$ 绕点C旋转任意角度，连接AD，BE，设AD，BE所在的直线交于点O，则在旋转过程中，始终有 $A D = B E$ ，且 $∠ A O B$ 的大小保持不变，这时点O到直线AB的最大距离为．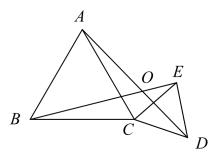

查看试题解析

三、综合题

13. 如图，已知给定等边△ABC及边AB上点D．

(1)、作经过点B，C，D的⊙O（要求：尺规作图，不写作法，保留作图痕迹并写出结论）．

(2)、若BC＝6，BD＝4，求OA的长．（说明：O为（1）小题所作圆的圆心）

查看试题解析
14. 已知菱形ABCD的边长为4．∠ADC=60°，等边△AEF两边分别交边DC，CB于点E，F．

(1)、特殊发现：如图1，若点E，F分别是边DC，CB的中点．求证：菱形ABCD对角线AC，BD的交点O即为等边△AEF的外心；

(2)、若点E，F始终分别在边DC，CB上移动，等边△AEF的外心为点P．
①猜想验证：如图2．猜想△AEF的外心P落在哪条直线上，并加以证明；

②学以致用：如图3，当△AEF的面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，求 $\frac{1}{D M} + \frac{1}{D N}$ 的值．

查看试题解析
15. 阅读材料：
“三角形的三个顶点确定一个圆，这个圆叫做三角形的外接圆、外接圆的圆心叫做三角形的外心，这个三角形叫做这个圆的内接三角形。”（苏科版《数学》九上 2.3确定圆的条件）

问题初探：

(1)、三角形的外心到三角形的距离相等

(2)、若点O是△ABC的外心，试探索∠BOC与∠BAC之间的数量关系。

(3)、如图，在Rt△ABC中，∠ACB=90°，AC=BC。将线段BC绕点B逆时针旋转30°到BD，连接AD、CD。用直尺和圆规在图中作出△BCD的外心O，并求∠ADB的度数。（保留作图痕迹，不写作法。）

查看试题解析
16. 等边△ABC与正方形DEFG如图1放置，其中D，E两点分别在AB，BC上，且BD＝BE．

(1)、求∠DEB的度数；

(2)、当正方形DEFG沿着射线BC方向以每秒1个单位长度的速度平移时，CF的长度y随着运动时间变化的函数图象如图2所示，且当t= $\sqrt{3}$ 时，y有最小值1；
①求等边△ABC的边长；
②连结CD，在平移的过程中，求当△CEF与△CDE同时为等腰三角形时t的值；
③从平移运动开始，到GF恰落在AC边上时，请直接写出△CEF外接圆圆心的运动路径的长度．

查看试题解析