【提升卷】3.4圆周角和圆心角的关系—北师大版数学九年级下册同步测试
试卷更新日期:2024-01-14 类型:同步测试
一、选择题
-
1. 如图,点在上, , 则( )
 A、48° B、24° C、22° D、21°2. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
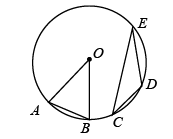
A、48° B、24° C、22° D、21°2. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )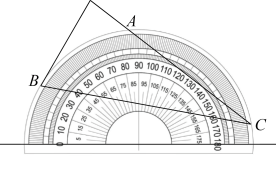 A、28° B、30° C、36° D、56°3. 如图,点A是中优弧的中点, , C为劣弧上一点,则的度数是( )
A、28° B、30° C、36° D、56°3. 如图,点A是中优弧的中点, , C为劣弧上一点,则的度数是( ) A、 B、 C、 D、4. 如图,△ABC内接于⊙O , ∠C=45°,AB=6,则⊙O半径为( )
A、 B、 C、 D、4. 如图,△ABC内接于⊙O , ∠C=45°,AB=6,则⊙O半径为( )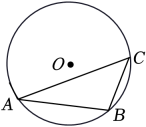 A、3 B、8 C、2 D、105. 如图,AB为⊙O的直径,C为AB上一点,AD∥OC , AD交⊙O于点D , 连接AC , CD , 设∠BOC=x°,∠ACD=y°,则下列结论成立的是( )
A、3 B、8 C、2 D、105. 如图,AB为⊙O的直径,C为AB上一点,AD∥OC , AD交⊙O于点D , 连接AC , CD , 设∠BOC=x°,∠ACD=y°,则下列结论成立的是( ) A、x+y=90 B、2x+y=90 C、2x+y=180 D、x=y6. 如图,四边形ABCD内接于⊙O , 已知点C为的中点,若∠A=50°,则∠CBD的度数为( )
A、x+y=90 B、2x+y=90 C、2x+y=180 D、x=y6. 如图,四边形ABCD内接于⊙O , 已知点C为的中点,若∠A=50°,则∠CBD的度数为( ) A、50° B、40° C、30° D、25°7. 如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若∠ECF=60°,则∠DCF的大小是 ( )
A、50° B、40° C、30° D、25°7. 如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若∠ECF=60°,则∠DCF的大小是 ( )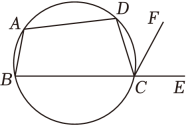 A、30° B、48° C、54° D、60°8. 如图,是的直径,内接于 , 延长在外相交于点 , 若 , 则的度数是( )
A、30° B、48° C、54° D、60°8. 如图,是的直径,内接于 , 延长在外相交于点 , 若 , 则的度数是( )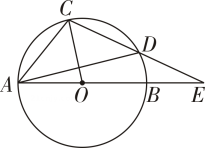 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=105°,则∠DCE的度数是°.
 10. 如图,在中, , 点D、E分别在上,且 , 将沿着折叠,点C恰好落在边上的点F处,如果 , 那么的长为
10. 如图,在中, , 点D、E分别在上,且 , 将沿着折叠,点C恰好落在边上的点F处,如果 , 那么的长为 11. 如图,为的直径, , 为的中点,过作∥交于 , 连接 , 则的度数为 .
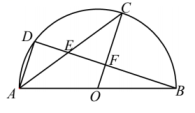
11. 如图,为的直径, , 为的中点,过作∥交于 , 连接 , 则的度数为 .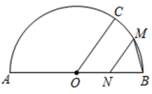 12. 如图,在中,为直径,点为圆上一点,将劣弧沿弦翻折交于点 , 连接 , 若点与圆心不重合, , 则的度数是 .
12. 如图,在中,为直径,点为圆上一点,将劣弧沿弦翻折交于点 , 连接 , 若点与圆心不重合, , 则的度数是 .
三、作图题
-
13. 如图是的正方形网格,请仅用无刻度直尺完成下列画图问题,保留作图痕迹.
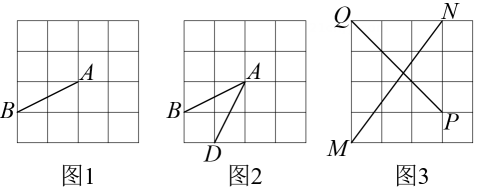 (1)、在图中,找一格点 , 连结 , 使画出一种即可 , 这样的格点与点不重合有 个
(1)、在图中,找一格点 , 连结 , 使画出一种即可 , 这样的格点与点不重合有 个
(2)、在图中,找一格点 , 连结、 , 使画出一种即可 .
(3)、在图中的线段上画一点 , 连结 , , 使 .四、解答题
-
14. 如图,AB是⊙O的直径,点C,D是AB同侧圆上两点,AC=BD,AD与BC交于点E,延长AD到F使DF=DE,连接BF.
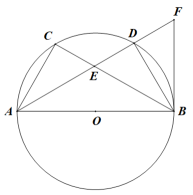 (1)、求证:CE=DE;(2)、若AD平分∠BAC,求证:BF为⊙O的切线.15. 如图,四边形ABCD内接于⊙O,∠BAD=90°, = . 过点C作CE⊥AD,垂足为E.
(1)、求证:CE=DE;(2)、若AD平分∠BAC,求证:BF为⊙O的切线.15. 如图,四边形ABCD内接于⊙O,∠BAD=90°, = . 过点C作CE⊥AD,垂足为E. (1)、求证:AE=CE.(2)、 若AE=3,DE= , 求∠'ABC的度数.
(1)、求证:AE=CE.(2)、 若AE=3,DE= , 求∠'ABC的度数.
-