【培优卷】3.4圆周角和圆心角的关系—北师大版数学九年级下册同步测试
试卷更新日期:2024-01-14 类型:同步测试
一、选择题
-
1. 如图,四边形内接于 , 交的延长线于点E,若平分 , , , 则( )
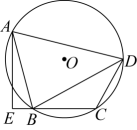 A、3 B、 C、 D、2. 如图,是的外接圆,弦交于点E, , , 过点O作于点F,延长交于点G,若 , , 则的长为( )
A、3 B、 C、 D、2. 如图,是的外接圆,弦交于点E, , , 过点O作于点F,延长交于点G,若 , , 则的长为( )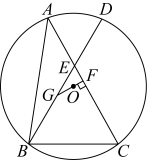 A、 B、7 C、8 D、3. 如图,AB为⊙O的直径,BC是弦,将绕着A点顺时针旋转得到 , 点D恰好落在⊙O上,AB交于E点,若OE=EB,AB=4,则BC的长是( )
A、 B、7 C、8 D、3. 如图,AB为⊙O的直径,BC是弦,将绕着A点顺时针旋转得到 , 点D恰好落在⊙O上,AB交于E点,若OE=EB,AB=4,则BC的长是( )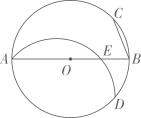 A、2 B、 C、 D、4. 如图,四边形为正方形,其中分别以为直径在正方形内部做半圆,正方形的对角线交于O点,点E是以为直径的半圆上的一个动点,则下列结论错误的是( )
A、2 B、 C、 D、4. 如图,四边形为正方形,其中分别以为直径在正方形内部做半圆,正方形的对角线交于O点,点E是以为直径的半圆上的一个动点,则下列结论错误的是( )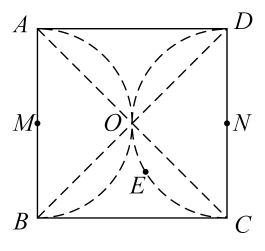 A、若正方形的边长为10,连接 , 则的最小值为 B、连接 , 则 C、连接 , 若 , , 则正方形的边长为 D、若M,N分别为的中点,存在点E,使得5. 如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
A、若正方形的边长为10,连接 , 则的最小值为 B、连接 , 则 C、连接 , 若 , , 则正方形的边长为 D、若M,N分别为的中点,存在点E,使得5. 如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )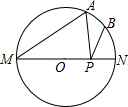 A、4 B、4 C、2 D、26. 等腰△ABC中,AB=AC,以腰AB为直径的圆O,与底边BC交于P,若圆O与腰AC的交点Q关于直线AP的对称点落在线段OA上(不与端点重合),则下列说法正确的是( )A、∠BAC>60° B、30°<∠ABC<60° C、BP>AB D、AC<PQ<AC7. 如图,内接于半径为的半圆中,为直径,点是的中点,连结交于点 , 平分交于点 , 为的中点,可得( )
A、4 B、4 C、2 D、26. 等腰△ABC中,AB=AC,以腰AB为直径的圆O,与底边BC交于P,若圆O与腰AC的交点Q关于直线AP的对称点落在线段OA上(不与端点重合),则下列说法正确的是( )A、∠BAC>60° B、30°<∠ABC<60° C、BP>AB D、AC<PQ<AC7. 如图,内接于半径为的半圆中,为直径,点是的中点,连结交于点 , 平分交于点 , 为的中点,可得( )
① ② ③ ④
A、①②③ B、①②④ C、①③④ D、②③④8. 我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,根据定义:①等边三角形一定是奇异三角形;②在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,则a:b:c=1::2;③如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.则△ACE是奇异三角形;④在③的条件下,当△ACE是直角三角形时,∠AOC=120°,其中,说法正确的有( ) A、①② B、①③ C、②④ D、③④
A、①② B、①③ C、②④ D、③④二、填空题
-
9. 如图,在平面直角坐标系xOy中,点B在x轴正半轴上,点D在y轴正半轴上,⊙C经过A,B,D,O四点,∠OAB=120°,OB=4 , 则点D的坐标是 .
 10. 已知内接于 , 它的内心为点 , 连接交弦于点 , 交于点 , 已知 , , , 则线段的长为 .
10. 已知内接于 , 它的内心为点 , 连接交弦于点 , 交于点 , 已知 , , , 则线段的长为 . 11. 如图,正方形ABCD的边长是4,F点是BC边的中点,点H是CD边上的一个动点,以CH为直径作 ,连接HF交 于E点,连接DE,则线段DE的最小值为.
11. 如图,正方形ABCD的边长是4,F点是BC边的中点,点H是CD边上的一个动点,以CH为直径作 ,连接HF交 于E点,连接DE,则线段DE的最小值为. 12. 如图,内接于⊙O, , 外角的平分线交⊙O于点D,若 , 则的度数为.
12. 如图,内接于⊙O, , 外角的平分线交⊙O于点D,若 , 则的度数为.

三、综合题
-
13. 如图,都是的半径, .
 (1)、求证:;(2)、若 , 求的半径.14. 已知四边形内接于 , 对角线是的直径.
(1)、求证:;(2)、若 , 求的半径.14. 已知四边形内接于 , 对角线是的直径. (1)、如图1,连接 , 若 , 求证;平分;(2)、如图2,为内一点,满足 , 若 , , 求弦的长.15. 在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:已知:是等边三角形,点D是内一点,连接 , 将线段绕C逆时针旋转得到线段 , 连接 , , , 并延长交于点F.当点D在如图所示的位置时:
(1)、如图1,连接 , 若 , 求证;平分;(2)、如图2,为内一点,满足 , 若 , , 求弦的长.15. 在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:已知:是等边三角形,点D是内一点,连接 , 将线段绕C逆时针旋转得到线段 , 连接 , , , 并延长交于点F.当点D在如图所示的位置时: (1)、观察填空:与全等的三角形是;(2)、利用(1)中的结论,求的度数(3)、判断线段 , , 之间的数量关系,并说明理由.
(1)、观察填空:与全等的三角形是;(2)、利用(1)中的结论,求的度数(3)、判断线段 , , 之间的数量关系,并说明理由.