【提升卷】3.3 垂径定理—2023-2024学年北师大版九年级下册同步测试
试卷更新日期：2024-01-14 类型：同步测试
一、选择题
-
1. 下列语句中：①平分弦的直径垂直于弦；②相等的圆心角所对的弧相等；③长度相等的两条弧是等弧；④圆是轴对称图形，任何一条直径都是它的对称轴；⑤在同圆或等圆中，如果两条弦相等，那么他们所对的圆周角相等，不正确的有（ ）A、2个 B、3个 C、4个 D、5个2. 如图，AB是⊙O的直径，C，D是⊙O上的两点，且BC平分∠ABD，AD分别与BC，OC相交于点E，F，则下列结论不一定成立的是（ ）
A、OC∥BD B、AD⊥OC C、△CEF≌△BED D、AF＝FD3. 如图所示，一圆弧过方格的格点 ， 试在方格中建立平面直角坐标系，使点的坐标为 ， 则该圆弧所在圆的圆心坐标是（ ）
A、 B、 C、 D、4. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，CD为⊙O的直径，弦AB⊥CD，垂足为点E，CE=1寸，AB=10寸，则直径CD的长度是 （ ）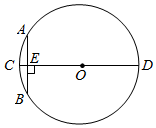
A、12寸 B、24寸 C、13寸 D、26寸5. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”意思是：今有一圆柱形木材，埋在墙壁中，不知大小，用锯子去锯这个木材，锯口深DE＝1寸，锯道AB＝1尺（1尺＝10寸），则这根圆柱形木材的直径是（ ）
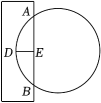A、12寸 B、13寸 C、24寸 D、26寸6. 已知⊙O的半径为5cm，在圆心O的同侧有两条互相平行的弦，长度分别为6cm和8cm，则这两条平行弦之间的距离是（ ）A、1cm． B、2cm． C、3cm． D、4cm．7. 如图，在半径为13 cm的圆形铁片上切下一块高为8cm的弓形铁片，则弦AB的长为（ ）．
A、10cm B、16cm C、24cm D、26cm8. 如图所示，AC是的直径，弦于点 ， 连结BC，过点作BC于点.若 ， 则OF的长为（ ）.
A、3 B、 C、2.5 D、二、填空题
-
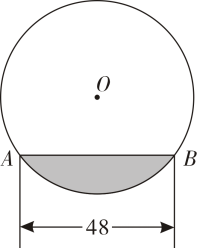
9. 往直径为的圆柱形容器内装入一些水以后，截面如图所示，且圆心在水面上方．若水面宽 ， 则水的最大深度为 ．
10. 如图，为的直径，弦 ， 垂足为 ， ， ， ， 则弦的长度为.
11. 如图，AB是⊙O的直径，弦CD⊥AB于点E，CD=AE=8cm，则OC的长为cm.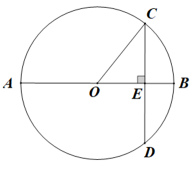
12. 小敏利用课余时间制作了一个脸盆架，如图①所示，图②是脸盆架的截面图，垂直放置的脸盆与架子的交点为A，B，AB=40 cm，脸盆的最低点C到AB的距离为10cm，则该脸盆的半径为cm．
三、作图题
-
13. 如图，一座石拱桥的形状是以点O为圆心，OA为半径的一段弧．
(1)、确定的中点C．(要求：尺规作图，只需保留作图痕迹，不必写作法和证明)(2)、若的度数为120° ，OA=10m，求石拱桥桥拱的高度．四、解答题
-
14. 如图，在以O为圆心的两个同心圆中，大圆的弦交小圆于C、D两点，若 ， ．
(1)、求的长；(2)、若大圆半径为 ， 求小圆的半径．
-
