【培优卷】3.3 垂径定理—北师大版数学九年级下册同步测试
试卷更新日期:2024-01-14 类型:同步测试
一、选择题
-
1. 如图,是的弦,点是上的动点(不与点 , 重合),过点作垂直于的弦 . 若设的半径为 , , , 则弦的长( )
 A、与 , , 的值均有关 B、只与 , 的值有关 C、只与的值有关 D、只与 , (或 , )的值有关2. 简车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示简车的一个盛水桶.如图2,当简车工作时,盛水桶的运行路径是以轴心0为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则简车工作时,盛水桶在水面以下的最大深度为( )m.
A、与 , , 的值均有关 B、只与 , 的值有关 C、只与的值有关 D、只与 , (或 , )的值有关2. 简车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示简车的一个盛水桶.如图2,当简车工作时,盛水桶的运行路径是以轴心0为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则简车工作时,盛水桶在水面以下的最大深度为( )m. A、1 B、2 C、3 D、43. 如图,圆心在轴的负半轴上,半径为5的与轴的正半轴交于点 , 过点的直线与相交于C,D两点.则弦CD长的所有可能的整数值有( )
A、1 B、2 C、3 D、43. 如图,圆心在轴的负半轴上,半径为5的与轴的正半轴交于点 , 过点的直线与相交于C,D两点.则弦CD长的所有可能的整数值有( ) A、1个 B、2个 C、3个 D、4个4. 如图所示,在中,为弦,交于点 . 且 . 为上任意一点,连接 , , 若的半径为 , 则的最大值为( )
A、1个 B、2个 C、3个 D、4个4. 如图所示,在中,为弦,交于点 . 且 . 为上任意一点,连接 , , 若的半径为 , 则的最大值为( ) A、 B、 C、 D、5. 已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )A、 B、4 C、 D、56. △ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为( )
A、 B、 C、 D、5. 已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )A、 B、4 C、 D、56. △ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为( ) A、 B、 C、 D、7. 如图,是的直径,分别以点O和点B为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M , N两点,直线与相交于C , D两点,若 , 则的长为( )
A、 B、 C、 D、7. 如图,是的直径,分别以点O和点B为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M , N两点,直线与相交于C , D两点,若 , 则的长为( ) A、 B、4 C、 D、8. 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
A、 B、4 C、 D、8. 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )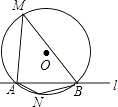 A、2 B、4 C、4 D、8
A、2 B、4 C、4 D、8二、填空题
-
9. 圆O的半径为5,为两条平行的弦, . 则这两条平行弦之间的距离为 .10. 如图,某公园有一月牙形水池,水池边缘有A , B , C , D , E五盏装饰灯.为了估测该水池的大小,观测员在A , D两点处发现点A , E , C和D , E , B均在同一直线上,沿AD方向走到F点,发现 . 测得米,米,米,则所在圆的半径为米,所在圆的半径为.米.
 11. 在平面直角坐标系中,我们定义点的“关联点”为 . 如果已知点在直线上,点在的内部,的半径长为(如图所示),那么点的横坐标的取值范围是 .
11. 在平面直角坐标系中,我们定义点的“关联点”为 . 如果已知点在直线上,点在的内部,的半径长为(如图所示),那么点的横坐标的取值范围是 . 12. 如图所示,抛物线 与x轴交于A、B两点,过点B的直线与抛物线交于点C(点C在x轴上方),过ABC三点的⊙M满足∠MBC=45°,则点C的坐标为.
12. 如图所示,抛物线 与x轴交于A、B两点,过点B的直线与抛物线交于点C(点C在x轴上方),过ABC三点的⊙M满足∠MBC=45°,则点C的坐标为.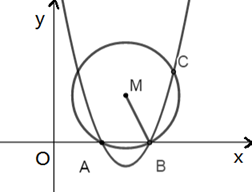
三、解答题
-
13. 如图1,装有水的水槽放置在水平桌面上,其横截面是以AB为直径的半圆O , AB=52cm , MN为水面截线,MN=48cm , GH为桌面截线,MN∥GH .
 (1)、作OC⊥MN于点C , 求OC的长;(2)、将图中的水倒出一部分得到图2,发现水面高度下降了14cm , 求此时水面截线减少了多少.14.
(1)、作OC⊥MN于点C , 求OC的长;(2)、将图中的水倒出一部分得到图2,发现水面高度下降了14cm , 求此时水面截线减少了多少.14. (1)、如图①,过⊙O上一点P作两条弦PA,PB.若PA=PB,则PO平分∠APB.为什么?(2)、如图②,若点P在⊙O内,过点P的两条弦AC,DB相等,则PO平分∠APB吗?为什么?(3)、如图③,若点P在⊙O外,过点P作PA,PB,分别交⊙O于点A,C和B,D,且AC=BD,则PO平分∠APB吗?为什么?
(1)、如图①,过⊙O上一点P作两条弦PA,PB.若PA=PB,则PO平分∠APB.为什么?(2)、如图②,若点P在⊙O内,过点P的两条弦AC,DB相等,则PO平分∠APB吗?为什么?(3)、如图③,若点P在⊙O外,过点P作PA,PB,分别交⊙O于点A,C和B,D,且AC=BD,则PO平分∠APB吗?为什么?四、实践探究题
-
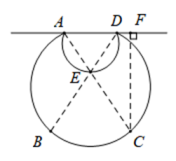
15. 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载(如图①):“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”

阅读完这段文字后,聪聪画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求“间径”就是要求⊙O的直径.根据上面记载的文字,发现AB= 寸,CD= 寸(一尺等于十寸).运用有关知识即可解决这个问题.请你补全题目条件,并帮助聪聪求出⊙O的直径.
16. 如图

 (1)、【基础巩固】
(1)、【基础巩固】
如图1,在△ABC中,D为AB上一点,AC2=AD•AB.求证:∠ACD=∠B.(2)、【尝试应用】
如图2,在平行四边形ABCD中,E是AB上一点,连结AC,EC.已知AE=4,AC=6,CD=9.求证:2AD=3EC.(3)、【拓展提高】
如图3,四边形ABCD内接于⊙O,AC、BD相交于点E,已知⊙O的半径为2,AE=CE,AB=AE,BD= , 求△ABD的面积.