2023-2024学年浙教版数学八年级(上)期末仿真模拟卷(杭州适用4)
试卷更新日期:2024-01-12 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 若某三角形两边的长分别是3和5,则此三角形第三边的长可能是( )A、2 B、3 C、8 D、12. 下列命题是真命题的是( )A、同位角相等 B、三个角分别相等的两个三角形全等 C、对顶角相等 D、三角形的一个外角大于任何一个内角3. 下列体育图标是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 根据下面的表述,能确定某地位置的是( )A、人民影院五排 B、距离学校3千米 C、北纬 , 东经 D、邮局南面5. 在平面直角坐标系中,点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 一本数学错题笔记本的售价为6元,若小青买本共付元,则和6分别是( )A、常量,变量 B、变量,常量 C、常量,常量 D、变量,变量7. 下列关于的函数中,是正比例函数的是( )A、 B、 C、 D、8. 设“○”“□”“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“○”"□”“△”按质量从小到大的排列顺序为( )
4. 根据下面的表述,能确定某地位置的是( )A、人民影院五排 B、距离学校3千米 C、北纬 , 东经 D、邮局南面5. 在平面直角坐标系中,点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 一本数学错题笔记本的售价为6元,若小青买本共付元,则和6分别是( )A、常量,变量 B、变量,常量 C、常量,常量 D、变量,变量7. 下列关于的函数中,是正比例函数的是( )A、 B、 C、 D、8. 设“○”“□”“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“○”"□”“△”按质量从小到大的排列顺序为( )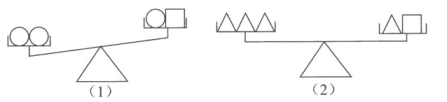 A、○□△ B、○△□ C、□○△ D、△□○9. 在△ABC中,∠ABC、∠ACB的角平分线交于点O,若90°<∠BOC<120°,则∠A的取值范围是( )
A、○□△ B、○△□ C、□○△ D、△□○9. 在△ABC中,∠ABC、∠ACB的角平分线交于点O,若90°<∠BOC<120°,则∠A的取值范围是( )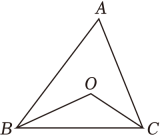 A、0°<∠A<30° B、10°<∠A<30° C、0°<∠A<60° D、10°<∠A<60°10. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )
A、0°<∠A<30° B、10°<∠A<30° C、0°<∠A<60° D、10°<∠A<60°10. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )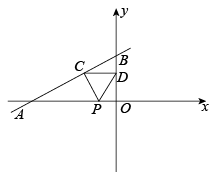 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
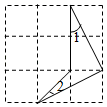
11. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=.
 12. 命题“如果 ab>0,那么a<0,b<0.”的逆命题是:.13. 若实数m使关于x的不等式组有解且至多有2个整数解,且使关于y的方程的解为非负数,则满足条件的所有整数m的和为 .14. 在平面直角坐标系中,关于x轴对称的点的坐标为.15. 如图,一次函数y1=kx+b与y2=mx+n的图象相交于点(1,3),则方程组的解为 , 关于x的不等式kx+b>mx+n的解为 .
12. 命题“如果 ab>0,那么a<0,b<0.”的逆命题是:.13. 若实数m使关于x的不等式组有解且至多有2个整数解,且使关于y的方程的解为非负数,则满足条件的所有整数m的和为 .14. 在平面直角坐标系中,关于x轴对称的点的坐标为.15. 如图,一次函数y1=kx+b与y2=mx+n的图象相交于点(1,3),则方程组的解为 , 关于x的不等式kx+b>mx+n的解为 .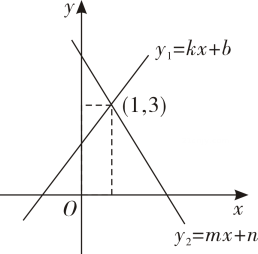 16. 在中, , , , 点 , 分别是边和上的动点,始终保持 , 连接 , , 则的最小值为。
16. 在中, , , , 点 , 分别是边和上的动点,始终保持 , 连接 , , 则的最小值为。
三、解答题(共7题,共66分)
-
17. 如图,△ABC与△DCE中,CA=CD , ∠1=∠2,BC=EC . 求证:∠A=∠D .
 18. 如图,在△ABC中,AB=BC,∠ABC=90°,D是边AC上一点,连接DB,过点C作CE⊥BD交BD于点E.
18. 如图,在△ABC中,AB=BC,∠ABC=90°,D是边AC上一点,连接DB,过点C作CE⊥BD交BD于点E.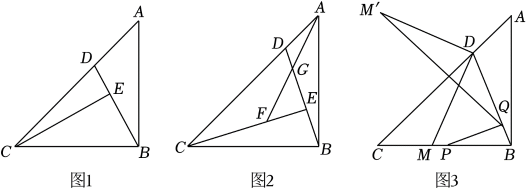 (1)、如图1,若∠DBC=4∠DCE , 求∠DCE的度数;(2)、如图2,在EC上截取EF=EB . 连接AF交BD于点G , 求证:CF=2EG;(3)、如图3,若 , 点D为线段AC上一点,点M是直线BC上一动点,连接MD,将线段MD绕点D顺时针旋转90°得到线段M′D,点P是线段BC的中点,点Q是线段BD上一个动点,连接PQ,M′Q,当PQ+M′Q最小时,请直接写PQ的长度.19. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长为28米长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=x米,花园面积S.
(1)、如图1,若∠DBC=4∠DCE , 求∠DCE的度数;(2)、如图2,在EC上截取EF=EB . 连接AF交BD于点G , 求证:CF=2EG;(3)、如图3,若 , 点D为线段AC上一点,点M是直线BC上一动点,连接MD,将线段MD绕点D顺时针旋转90°得到线段M′D,点P是线段BC的中点,点Q是线段BD上一个动点,连接PQ,M′Q,当PQ+M′Q最小时,请直接写PQ的长度.19. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长为28米长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=x米,花园面积S. (1)、写出S 关于x的函数解析式,当S=192平方米,求x的值;(2)、若在P处有一棵树与墙CD、AD的距离分别是15米和6米,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.20. 如图
(1)、写出S 关于x的函数解析式,当S=192平方米,求x的值;(2)、若在P处有一棵树与墙CD、AD的距离分别是15米和6米,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.20. 如图 (1)、在平面直角坐标系中,画 , 使其三个顶点为 , , ;(2)、是直角三角形吗?请证明你的判断.21. 假期将至,金华某旅行社准备打印一些照片进行宣传,某打印店现推出活动如下:“方式A”使用者先交50元会员费,然后每打印一张,再付0.4元;“方式B”免交会员费,每打印一张,付0.6元.若本次打印x张,两种方式的费用分别为元和元.(1)、写出 , 与x之间的函数关系式.(2)、当打印多少张时两种方式的费用相同?并说明相应理由.(3)、如果此次打印不超过150张,请你为其选一种便宜的打印方式;如果不低于300张,请你为其选种便宜的打印方式.22. 综合与探究:
(1)、在平面直角坐标系中,画 , 使其三个顶点为 , , ;(2)、是直角三角形吗?请证明你的判断.21. 假期将至,金华某旅行社准备打印一些照片进行宣传,某打印店现推出活动如下:“方式A”使用者先交50元会员费,然后每打印一张,再付0.4元;“方式B”免交会员费,每打印一张,付0.6元.若本次打印x张,两种方式的费用分别为元和元.(1)、写出 , 与x之间的函数关系式.(2)、当打印多少张时两种方式的费用相同?并说明相应理由.(3)、如果此次打印不超过150张,请你为其选一种便宜的打印方式;如果不低于300张,请你为其选种便宜的打印方式.22. 综合与探究:如图1,平面直角坐标系中,一次函数的图象分别交x轴、y轴于点A , B , 一次函数的图象经过点A , 并与y轴交于点C.
 (1)、写出A , B两点的坐标及k的值;(2)、如图2,若点P是x轴正半轴上的一个动点,过点P作轴x的垂线,分别交直线 , 于点M , N.设点P的横坐标为m().
(1)、写出A , B两点的坐标及k的值;(2)、如图2,若点P是x轴正半轴上的一个动点,过点P作轴x的垂线,分别交直线 , 于点M , N.设点P的横坐标为m().①当点P在线段上时,用含m的代数式表示线段的长为 ;
②作点M关于x轴的对称点 , 在点P运动过程中,当时,求点P的坐标.
23.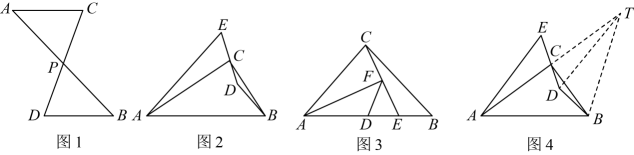 (1)、【思维启迪】
(1)、【思维启迪】如图1,点P是线段 , 的中点,则与的数量关系为 , 位置关系为;
(2)、【思维探索】如图2,在中, , 点D为内一点,连接 , , 延长到点E , 使 , 连接 , 若 , 请用等式表示 , , 之间的数量关系,并说明理由;
★小明思考良久后,根据这一条件,给出了如图4的辅助线:延长到T , 使得 , 连接 , , 请你根据小明给出的辅助线,继续猜想 , , 之间的数量关系,并说明理由.
(3)、如图3,在中, , , 点D为中点,点E在线段上(点E不与点B , 点D重合),连接 , 过点A作 , 连接 , 若 , , 请求出的长.