江苏省淮安市2022-2023学年高一上学期期末 数学试题
试卷更新日期:2024-01-12 类型:期末考试
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 命题“ , 都有”的否定为( )A、 , 使得 B、 , 使得 C、 , 都有 D、 , 都有3. 已知 , 若集合 , , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 甲、乙、丙三位同学被问到是否去过淮安方特、龙宫大白鲸世界、西游乐园三个景点时,甲说:我去过的景点比乙多,但没去过淮安方特;乙说:我没去过龙宫大白鲸世界;丙说:我们三个人去过同一个景点.则乙一定去过的景点是( )A、淮安方特 B、龙宫大白鲸世界 C、西游乐园 D、不能确定5. 已知 , , , 则m、n、p的大小关系为( )A、 B、 C、 D、6. 我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔离分家万事休.”在数学学习和研究中,常用函数的图象来研究函数性质,也常用函数解析式来琢磨函数的图象特征,函数的部分图象大致为( )A、
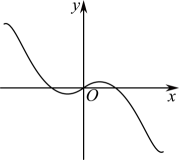 B、
B、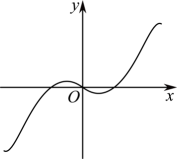 C、
C、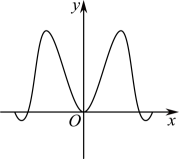 D、
D、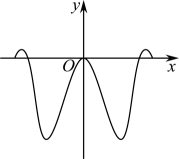 7. 已知函数在内有一个零点,且求得的部分函数值数据如下表所示:
7. 已知函数在内有一个零点,且求得的部分函数值数据如下表所示:0
1
0.5
0.75
0.625
0.5625
0.6875
0.65625
0.671875
-1
1
-0.375
0.1718
-0.1308
-0.2595
0.01245
-0.06113
-0.02483
要使零点的近似值精确到0.1,则对区间的最少等分次数和近似解分别为( )
A、6次0.7 B、6次0.6 C、5次0.7 D、5次0.68. 已知函数 , 若不等式对恒成立,则实数的取值范围为( )A、 B、 C、 D、二、选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
-
9. 下列结论中正确的有( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , , 且 , 则的最小值为410. 已知有两个零点 , 且 , 则下列说法正确的有( )A、 , B、 C、若 , 则的最小值为 D、且 , 都有11. 对于函数 , 下列结论正确的有( )A、当时,的图像关于点中心对称 B、当时,在区间上是单调函数 C、若恒成立,则的最小值为2 D、当时,的图象可由的图象向右平移个单位长度得到12. 已知函数是定义在上的偶函数,对于任意 , 都有成立.当时, , 下列结论中正确的有( )A、 B、函数在上单调递增 C、直线是函数的一条对称轴 D、关于的方程共有4个不等实根
三、填空题:本题共4小题,每小题5分,共20分.
-
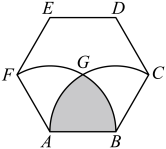
13. 函数 , 则 .14. 已知a , b为正实数,满足 , 则的最小值为 .15. 如图,正六边形的边长为 , 分别以点为圆心,长为半径画弧,两弧交于点 , 则围成的阴影部分的面积为 .
 16. 近年来,淮安市依托地方资源优势,用风能等清洁能源替代传统能源,因地制宜实施新能源项目,在带来了较好经济效益的同时,助力了本地农户增收致富.目前利用风能发电的主要手段是风车发电.如图,风车由一座塔和三个叶片组成,每两个叶片之间的夹角均为 , 现有一座风车,塔高90米,叶片长40米.叶片按照逆时针方向匀速转动,并且每6秒旋转一圈,风车开始旋转时某叶片的一个端点P在风车的最低点(此时P离地面50米).设点P转动t(秒)后离地面的距离为S(米),则S关于t的函数关系式为 , 叶片旋转一圈内点P离地面的高度不低于70米的时长为秒.
16. 近年来,淮安市依托地方资源优势,用风能等清洁能源替代传统能源,因地制宜实施新能源项目,在带来了较好经济效益的同时,助力了本地农户增收致富.目前利用风能发电的主要手段是风车发电.如图,风车由一座塔和三个叶片组成,每两个叶片之间的夹角均为 , 现有一座风车,塔高90米,叶片长40米.叶片按照逆时针方向匀速转动,并且每6秒旋转一圈,风车开始旋转时某叶片的一个端点P在风车的最低点(此时P离地面50米).设点P转动t(秒)后离地面的距离为S(米),则S关于t的函数关系式为 , 叶片旋转一圈内点P离地面的高度不低于70米的时长为秒.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17.(1)、已知 , 求的值;(2)、求值 .18. 设全集为 , 集合 , .
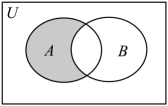 (1)、当时,求图中阴影部分表示的集合C;(2)、在①;②;③这三个条件中任选一个作为已知条件,求实数a的取值范围.19. 已知函数的部分图象如图所示.
(1)、当时,求图中阴影部分表示的集合C;(2)、在①;②;③这三个条件中任选一个作为已知条件,求实数a的取值范围.19. 已知函数的部分图象如图所示. (1)、求函数的解析式;(2)、将函数的图象向左平移个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)得到函数的图象,若关于x的方程在区间上有两个不同的实数解,求实数a的取值范围.20. 2022年新冠肺炎疫情仍在世界好多国家肆虐,目前的新冠病毒是奥密克戎变异株,其特点是:毒力显著减弱,但传染性很强,绝大多数人感染后表现为无症状或轻症,重症病例很少,长期一段时间以来全国没有一例死亡病例.某科研机构对奥密克戎变异株在特定环境下进行观测,每隔单位时间T进行一次记录,用x表示经过的单位时间数,用y表示奥密克戎变异株感染人数,得到如下观测数据:
(1)、求函数的解析式;(2)、将函数的图象向左平移个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)得到函数的图象,若关于x的方程在区间上有两个不同的实数解,求实数a的取值范围.20. 2022年新冠肺炎疫情仍在世界好多国家肆虐,目前的新冠病毒是奥密克戎变异株,其特点是:毒力显著减弱,但传染性很强,绝大多数人感染后表现为无症状或轻症,重症病例很少,长期一段时间以来全国没有一例死亡病例.某科研机构对奥密克戎变异株在特定环境下进行观测,每隔单位时间T进行一次记录,用x表示经过的单位时间数,用y表示奥密克戎变异株感染人数,得到如下观测数据:1
2
3
4
5
6
…
(人数)
…
6
…
36
…
216
…
若奥密克戎变异株的感染人数y与经过个单位时间T的关系有两个函数模型与可供选择.
(参考数据: , , , )
(1)、判断哪个函数模型更合适,并求出该模型的解析式;(2)、求至少经过多少个单位时间该病毒的感染人数不少于1万人.