河北省沧州市泊头市2023-2024学年高一上学期1月数学期末考试试卷

试卷更新日期：2024-01-12 类型：期末考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符题目要求的．

1. 已知集合 $A = {x | x^{2} - x - 2 \leq 0}$ ， $B = {x | \frac{1}{3} < 3^{x} \leq 27}$ ，则 $A ∩ B =$ （）

A、 ${x | ∣ - 1 \leq x \leq 3}$ B、 ${x | - 1 \leq x \leq 2}$ C、 ${x | - 1 < x \leq 2}$ D、 ${x | - 1 < x \leq 3}$

查看试题解析
2. 命题“ $\forall x \in R$ ， $x^{2} - 2 x \geq - 1$ ”的否定是（）

A、 $\exists x \in R$ ， $x^{2} - 2 x \leq - 1$ B、 $\forall x \in R$ ， $x^{2} - 2 x < - 1$ C、 $\exists x \in R$ ， $x^{2} - 2 x < - 1$ D、 $\forall x \in R$ ， $x^{2} - 2 x \leq - 1$

查看试题解析
3. 已知点 $P (3 ， 4)$ 是角 $α$ 的终边上一点，则 $s i n (α + \frac{π}{6}) =$ （）

A、 $\frac{4 \sqrt{3} - 3}{10}$ B、 $\frac{4 \sqrt{3} + 3}{10}$ C、 $\frac{- 4 \sqrt{3} + 3}{10}$ D、 $\frac{3 \sqrt{3} + 4}{10}$

查看试题解析
4. 已䂑 $a = s i n 55 °$ ， $b = s i n 110 °$ ， $c = t a n 55 °$ ，则a ， b ， c的大小关系为（）

A、 $a < b < c$ B、 $a < c < b$ C、 $b < a < c$ D、 $b < c < a$

查看试题解析
5. 定义在 $R$ 上的函数 $f (x)$ 是偶函数的一个必要不充分条件为（）

A、 $f (0) = 0$ B、 $f (- 2) = f (2)$ C、 $f (- x) = f (x)$ D、 $f (| x |) = f (x)$

查看试题解析
6. 已知 $x_{1}$ ， $x_{2}$ 是方程 $| l g x | = t$ 的两个不等实根，则 $\frac{2}{x_{1}} + \frac{1}{x_{2}}$ 的最小值是（）

A、2 B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、3

查看试题解析
7. 已知函数 $f (x) = s i n ω x + c o s ω x (ω > 0)$ ，若 $f (x)$ 在 $(0 ， π)$ 上有3个零点，则 $ω$ 的取值范围是（）

A、 $[\frac{9}{4} ， \frac{13}{4})$ B、 $(\frac{9}{4} ， \frac{13}{4}]$ C、 $[\frac{11}{4} ， \frac{15}{4})$ D、 $(\frac{11}{4} ， \frac{15}{4}]$

查看试题解析
8. 已知定义在 $(- \frac{π}{2} ， \frac{π}{2})$ 上的函数 $f (x) = x^{3} + t a n x + 2$ ，则不等式 $f (x - 2) + f (\frac{x}{2}) > 4$ 的解集是（）

A、 $(\frac{4}{3} ， + \infty)$ B、 $(2 - \frac{π}{2} ， π)$ C、 $(\frac{4}{3} ， π)$ D、 $(\frac{4}{3} ， \frac{π}{2} + 2)$

查看试题解析

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

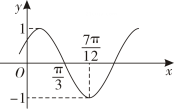
9. 为了得到函数 $f (x) = s i n (2 x - \frac{2 π}{3})$ 的图象，只需把正弦曲线上所有的点（）

A、先向右平移 $\frac{2 π}{3}$ 个单位长度，再将横坐标缩短到原米的 $\frac{1}{2}$ ，纵坐标不变 B、先向右平移 $\frac{π}{3}$ 个单位长度，再将横坐标伸长到原来的2倍，纵坐标不变 C、先将横坐标缩短到原来的 $\frac{1}{2}$ ，纵坐标不变，再向右平移 $\frac{π}{3}$ 个单位长度 D、先将横坐标伸长到原来的2倍，纵坐标不变，再向右平移 $\frac{π}{3}$ 个单位长度

查看试题解析
10. 下列说法正确的是（）

A、若幂函数的图象经过点 $(4 ， \frac{1}{2})$ ，则函数的解析式为 $y = x^{- \frac{1}{2}}$ B、若函数 $f (x) = x^{- 2}$ ，则 $f (x)$ 在区间 $(- \infty ， 0)$ 上单调递减 C、若正实数m ， n满足 $m^{\frac{1}{2}} > n^{\frac{1}{2}}$ ，则 $m^{- \frac{1}{2}} < n^{- \frac{1}{2}}$ D、若函数 $f (x) = x^{- 1}$ ，则对任意 $x_{1}$ ， $x_{2} \in (- \infty ， 0)$ ，且 $x_{1} \neq x_{2}$ ，有 $\frac{f (x_{1}) + f (x_{2})}{2} <$ $f (\frac{x_{1} + x_{2}}{2})$

查看试题解析
11. 摩天轮是一种大型转轮状的机械建筑设施，上面挂在轮边缘的是供乘客搭乘的座舱．某地一摩天轮与地面的垂直高度（最高处与地面的距离）为208米，直径193米，入口在最底部．摩天轮逆时针方向匀速转动，30分钟转一圈，假设该摩天轮共有36个座舱，且每两个座舱间隔相等，则下列说法正确的是（）

A、若摩天轮的转速减半，则其旋转一圈的时间是原来的一半 B、乘客从入口进入座舱，摩天轮开始转动后，乘客距离水平地面的高度 $h ($ 米）与时间 $t$ （分钟）的函数解析式为 $h (t) = 96.5 s i n (\frac{π}{15} t - \frac{π}{2}) + 111.5$ C、乘客从入口进入座舱，摩天轮开始转动后，经过10分钟，乘客距离地面的高度为63.25米 D、游客乙在游客甲后进入座舱，且中间间隔5个座舱，在摩天轮转动一周的过程中，两人距离地面的高度差的最大值为96.5米

查看试题解析
12. 已知函数 $f (x)$ 为 $R$ 上的奇函数，当 $x > 0$ 时， $f (x) = l n x$ ，记 $h (x) = f (x) s i n x +$ $s i n x t a n x$ ，则下列结论正确的是（）

A、 $h (x)$ 是偶函数 B、当 $x < 0$ 时， $f (x) = - l n (- x)$ C、 $h (x)$ 在区间 $[0 ， 2 π]$ 上有3个零点 D、 $h (x)$ 大于0的零点从小到大排列依次为 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， …，则 $\frac{3 π}{2} < x_{2} + x_{3} < 2 π$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分．

13. 已知一个扇形的圆心角为2．其周长的值等于面积的值，则扇形的半径 $r =$ ．

查看试题解析
14. 已知 $c o s (α - \frac{π}{3}) = \frac{2}{3}$ ，则 $s i n (\frac{5 π}{6} - α) =$ ．

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} l o g_{\frac{1}{2}} (x^{2} + a x + 3) ， x \geq 2 ， \\ a x - 2 a ， x < 2 \end{array}$ 在 $R$ 上单调递减，则实数 $a$ 的取值范围为．

查看试题解析
16. 若不等式 $l g \frac{1 + (3 - t) 3^{x}}{4} \geq (x - 1) l g 4$ 对于任意 $x \in (- \infty ， 1)$ 恒成立，则实数 $t$ 的取值范围是．

查看试题解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17. 求下列各式的值：

(1)、 $(l g 5)^{2} + 2 l g 2 - (l g 2)^{2} + {(\frac{8}{27})}^{- \frac{2}{3}}$ ；

(2)、 $\frac{t a n (π + α) c o s (- α) s i n (\frac{3 π}{2} + α)}{c o s (π - α) s i n (- π - α)}$ ．

查看试题解析
18. 已知函数 $f (x) = {(l o g_{\frac{1}{2}} x)}^{2} - 3 l o g_{\frac{1}{2}} x - 4$ ．

(1)、若 $f (x) \leq 0$ ，求 $x$ 的取值范围；

(2)、当 $\frac{1}{8} \leq x \leq 4$ 时，求函数 $f (x)$ 的值域．

查看试题解析
19. 已知 $α \in (0 ， π)$ ．

(1)、若 $s i n α + c o s α = \frac{2}{5}$ ，求 $s i n α c o s α$ 的值；

(2)、求 $y = s i n α c o s α + s i n α + c o s α$ 的值域．

查看试题解析
20. 已知函数 $f (x) = \frac{e^{x} + t}{e^{x} - t}$ 是定义在 $R$ 上的奇函数．

(1)、求 $t$ 的值，并判断函数 $f (x)$ 的单调性（给出判断即可，不需要证明）；

(2)、若对于任意 $x > 0$ ， $y > 0$ ，且 $x + 2 y = 1$ ，都有 $f (2^{λ + 2 x y}) < f (2^{x^{2} + 2 y})$ 恒成立，求实数 $λ$ 的取值范围．

查看试题解析
21. 已知函数 $f (x) = c o s (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 的部分图象如图所示．

(1)、求 $f (x)$ 的解析式；

(2)、若 $g (x) = s i n (2 x + \frac{π}{4})$ ，是否存在实数 $λ$ ， $\forall x_{1} \in [- \frac{π}{3} ， \frac{π}{3}]$ ， $\exists x_{2} \in [- \frac{11 π}{24} ， \frac{5 π}{24}]$ ，使得 $λ - f (x_{1}) = g (x_{2})$ 成立?若存在．求出 $λ$ 的取值范围；若不存在，请说明理内．

查看试题解析
22. 如图所示，某小区中心有一块圆心角为 $60 °$ ，半径为 $8 \sqrt{3} m$ 的扇形空地，现计划将该区域设计成亲子室外游乐区域，根据设计要求，需要铺设一块平行四边形的塑胶地面EFPQ（其中点E ， F在边OA上，点 $Q$ 在边OB上，点 $P$ 在AB上），其他区域地面铺设绿地，设 $∠ P O A = θ$ .

(1)、 $θ$ 表示绿地的面积 $S$ ；

(2)、若铺设绿地每平分米100元，要使得铺设绿地的出用 $W$ 最低， $θ$ 应取何值，并求出此时 $W$ 的值．

查看试题解析