江苏省海安市2022-2023学年高一上学期期末 数学试题
试卷更新日期:2024-01-12 类型:期末考试
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知全集 , 集合 , 则( )A、 B、 C、 D、2. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,3. 式子的值为( )A、 B、 C、 D、14. 图中实线是某景点收支差额关于游客量的图像,由于目前亏损,景点决定降低成本,同时提高门票价格,决策后的图像用虚线表示,以下能说明该事实的是( )A、
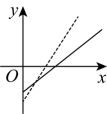 B、
B、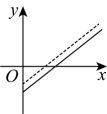 C、
C、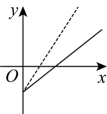 D、
D、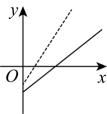 5. 若是的必要不充分条件,是的充分不必要条件,则是的( )A、充分不必要条件 B、充要条件 C、必要不充分条件 D、既不充分也不必要条件6. 将函数的图象向左平移个单位长度后,所得图象关于原点对称,则的最小值为( )A、 B、 C、 D、7. 已知函数 , 记 , , , 则( )A、 B、 C、 D、8. 已知函数满足:对任意的非零实数x , y , 都成立,.若 , , 则( )A、 B、 C、2 D、3
5. 若是的必要不充分条件,是的充分不必要条件,则是的( )A、充分不必要条件 B、充要条件 C、必要不充分条件 D、既不充分也不必要条件6. 将函数的图象向左平移个单位长度后,所得图象关于原点对称,则的最小值为( )A、 B、 C、 D、7. 已知函数 , 记 , , , 则( )A、 B、 C、 D、8. 已知函数满足:对任意的非零实数x , y , 都成立,.若 , , 则( )A、 B、 C、2 D、3二、选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 若 , 则( )A、 B、 C、 D、10. 记无理数小数点后第n位上的数字为m , 则m是关于n的函数,记作 , 其定义域为A , 值域为B , 则( )A、 B、函数的图象是一群孤立的点 C、n是关于m的函数 D、11. 奇函数与偶函数的定义域均为 , 在区间上都是增函数,则( )A、 B、在区间上是增函数,在区间上是减函数 C、是奇函数,且在区间上是增函数 D、不具有奇偶性,且在区间上的单调性不确定12. 我们知道,每一个音都是由纯音合成的,纯音的数学模型是.已知某音是由3个不同的纯音合成,其函数为 , 则( )A、是奇函数 B、的最小正周期为 C、在上是单调增函数 D、的最大值为
三、填空题:本大题共4小题,每小题5分,共20分.
-
13. 已知扇形的半径为1cm,弧长为2cm,则其圆心角所对的弦长为cm.14. 在平面直角坐标系中,已知角的终边经过点 , 若角的终边与角的终边关于轴对称,则.15. 已知圆和四边形(四个角均为直角)的周长相等,面积分别为 , , 则的最小值为.16. 已知函数在区间上是减函数,则的取值集合为.(用列举法表示)
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 已知集合 , 集合(1)、若 , 求;(2)、若 , 求的取值范围.18. 已知.(1)、若 , 求的值;(2)、若 , 求的值.19. 已知函数的振幅为 , 最小正周期为 , 且其恰满足条件①②③中的两个条件:
①初相为②图像的一个最高点为③图像与轴的交点为
(1)、求的解析式(2)、若 , 求的值.20. 设计一个印有“红十字”logo的正方形旗帜(如图).要求“红十字”logo居中,其突出边缘之间留空宽度均为2cm,“红十字”logo的面积(阴影部分)为.的长度不小于的长度.记 , .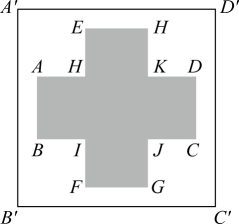 (1)、试用表示 , 并求出的取值范围;(2)、当为多少时,可使正方形的面积最小?
(1)、试用表示 , 并求出的取值范围;(2)、当为多少时,可使正方形的面积最小?参考结论:函数在上是减函数