湖南省娄底市双峰县2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2024-01-12 类型:期中考试
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列方程一定是一元二次方程的是( )A、 B、5x2﹣6y﹣3=0 C、ax2﹣x+2=0 D、(a2+1)x2+bx+c=02. 已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E , 过点E作AB的平行线交BC于点F . 则下列说法不正确的是( )
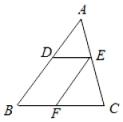 A、 B、 C、 D、3. 三角形的面积为12cm2 , 这时底边上的高ycm底边xcm之间的函数关系用图象表示大致是( )A、
A、 B、 C、 D、3. 三角形的面积为12cm2 , 这时底边上的高ycm底边xcm之间的函数关系用图象表示大致是( )A、 B、
B、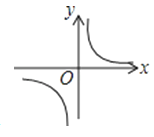 C、
C、 D、
D、 4. 已知线段AB的长度为2,点C是线段AB的黄金分割点,则AC的长度为( )A、 B、 C、﹣1或3- D、或﹣25. 用配方法解一元二次方程2x2﹣3x﹣1=0,配方正确的是( )A、 B、 C、 D、6. 如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为( )
4. 已知线段AB的长度为2,点C是线段AB的黄金分割点,则AC的长度为( )A、 B、 C、﹣1或3- D、或﹣25. 用配方法解一元二次方程2x2﹣3x﹣1=0,配方正确的是( )A、 B、 C、 D、6. 如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为( ) A、x>﹣2 B、﹣2<x<0或x>1 C、x>1 D、x<﹣2或0<x<17. 如图,是边边上的两点,且 , 若 , 则与的周长之比为( )
A、x>﹣2 B、﹣2<x<0或x>1 C、x>1 D、x<﹣2或0<x<17. 如图,是边边上的两点,且 , 若 , 则与的周长之比为( ) A、 B、 C、 D、8. 如图,小正方形的边长为1,则下列图中的三角形与△ABC相似的是( )
A、 B、 C、 D、8. 如图,小正方形的边长为1,则下列图中的三角形与△ABC相似的是( ) A、
A、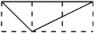 B、
B、 C、
C、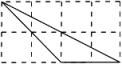 D、
D、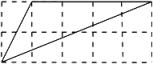 9. 如图,一长为32m、宽为20m的矩形地面上修建有同样宽的道路(图中阴影部分),余下部分进行了绿化.若已知绿化面积为540m2 , 道路宽度为x m , 则题中涉及的等量关系式为( )
9. 如图,一长为32m、宽为20m的矩形地面上修建有同样宽的道路(图中阴影部分),余下部分进行了绿化.若已知绿化面积为540m2 , 道路宽度为x m , 则题中涉及的等量关系式为( ) A、(32﹣x)(20﹣x)=540 B、(x﹣32)(20﹣x)=540 C、(x﹣32)(x﹣20)=540 D、(32×24)﹣(32x+20x)=54010. 如图,在平面直角坐标系中,点A在函数y=﹣(x<0)的图象上,点B在函数y=(x>0)的图象上,若AO=2BO , ∠AOB=90°,则k的值为( )
A、(32﹣x)(20﹣x)=540 B、(x﹣32)(20﹣x)=540 C、(x﹣32)(x﹣20)=540 D、(32×24)﹣(32x+20x)=54010. 如图,在平面直角坐标系中,点A在函数y=﹣(x<0)的图象上,点B在函数y=(x>0)的图象上,若AO=2BO , ∠AOB=90°,则k的值为( ) A、1 B、2 C、1.5 D、0.25
A、1 B、2 C、1.5 D、0.25二、填空题(本大题共6小题,共18分)
-
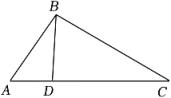
11. 如果 , 那么的值等于 .12. 已知x1、x2是一元二次方程x2﹣4x﹣7=0的两个实数根,则的值是 .13. 如图,在△ABC中,D为边AC上的点,连接BD , 添加一个条件: , 可以使得△ADB∽△ABC . (只需写出一个)
 14. 关于x的一元二次方程(m﹣1)x2+3x+m2﹣1=0的一根为0,则m的值是 .15. 反比例函数 的图象在第二、四象限,则m的取值范围是.16. 如图,在△ABC中,AD⊥BC于点D , 正方形EFGH的四个顶点都在△ABC的边上,若BC=6cm , AD=4cm , 则正方形EFGH的边长是cm .
14. 关于x的一元二次方程(m﹣1)x2+3x+m2﹣1=0的一根为0,则m的值是 .15. 反比例函数 的图象在第二、四象限,则m的取值范围是.16. 如图,在△ABC中,AD⊥BC于点D , 正方形EFGH的四个顶点都在△ABC的边上,若BC=6cm , AD=4cm , 则正方形EFGH的边长是cm .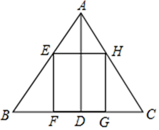
三、计算题(每小题6分,共18分)
-
17. 解方程:(1)、x2﹣6x+9=(5﹣2x)2;(2)、2(x﹣2)=x2﹣4.18. 已知某品牌显示器的寿命大约为2×104小时.(1)、这种显示器可工作的天数d与平均每日工作的小时数t之间具有怎样的函数关系?(2)、如果平均每天工作10小时,则这种显示器大约可使用多长时间?19. 已知关于x的方程x2+ax+a﹣2=0.(1)、若该方程的一个根为1,求a的值;(2)、若a的值为3时,请解这个方程.
四、解答题(每小题8分,共16分)
-
20. 如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC , AE∥DF , , BF=6cm , 求EF和FC的长.
 21. 已知反比例函数 与一次函数y=kx+b(k≠0)交于点A(﹣1,6)、B(n , 2).
21. 已知反比例函数 与一次函数y=kx+b(k≠0)交于点A(﹣1,6)、B(n , 2). (1)、求反比例函数与一次函数的表达式;(2)、若点A关于y轴的对称点为A′,连接AA′,BA′,求△AA′B的面积.
(1)、求反比例函数与一次函数的表达式;(2)、若点A关于y轴的对称点为A′,连接AA′,BA′,求△AA′B的面积.五、解答题(每小题9分,共18分)
-
22. 如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(﹣4,3).
 (1)、以点O为位似中心,在给定的网格中画出△A1B1C1 , 使△ABC与△A1B1C1位似,并且点A1的坐标为(8,﹣6).(2)、△ABC与△A1B1C1的位似比是 .(3)、△A1B1C1的面积是 .23. “阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种,在双峰县城南郊区李大叔承包了一个葡萄园,种植了大量“阳光玫瑰葡萄”,县城某品牌水果经销商计划在2023年五一期间进行商业促销活动,经过调查往年的统计数据发现,李大叔批发“阳光玫瑰葡萄”的最低价格为每斤15元.若按每斤30元的价格到市区销售,平均每天可售出60斤.若每斤“阳光玫瑰葡萄”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.(1)、若降价2元,则每天的销售利润是多少元?(2)、若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元,那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元?(其它成本忽略不计)
(1)、以点O为位似中心,在给定的网格中画出△A1B1C1 , 使△ABC与△A1B1C1位似,并且点A1的坐标为(8,﹣6).(2)、△ABC与△A1B1C1的位似比是 .(3)、△A1B1C1的面积是 .23. “阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种,在双峰县城南郊区李大叔承包了一个葡萄园,种植了大量“阳光玫瑰葡萄”,县城某品牌水果经销商计划在2023年五一期间进行商业促销活动,经过调查往年的统计数据发现,李大叔批发“阳光玫瑰葡萄”的最低价格为每斤15元.若按每斤30元的价格到市区销售,平均每天可售出60斤.若每斤“阳光玫瑰葡萄”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.(1)、若降价2元,则每天的销售利润是多少元?(2)、若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元,那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元?(其它成本忽略不计)六、综合题(每小题10分,共20分)
-
24. 已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0.(1)、求证:方程有两个不相等的实数根;(2)、如果方程的两实根为x1、x2 , 且﹣x1x2=27,求m的值.25. 如图1,在等腰直角三角形ADC中,∠ADC=90°,AD=4.点E是AD的中点,以DE为边作正方形DEFG , 连接AG , CE . 将正方形DEFG绕点D顺时针旋转,旋转角为α(0°<α<90°).
 (1)、如图2,在旋转过程中,
(1)、如图2,在旋转过程中,①判断△AGD与△CED是否全等,并说明理由;
②当CE=CD时,AG与EF交于点H , 求GH的长.
(2)、如图3,延长CE交直线AG于点P .①求证:AG⊥CP;
②在旋转过程中,线段PC的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.