江西省景德镇市乐平市2023-2024学年八年级上学期11月期中数学试题
试卷更新日期:2024-01-12 类型:期中考试
一、选择题(共6小题,每小题3分,共18分)
-
1. 下列条件中,不能判定△ABC是直角三角形的是( )A、∠A=∠B+∠C B、a:b:c=5:12:13 C、a2=(b+c)(b-c) D、∠A:∠B:∠C=3:4:52. 下列四个实数1,-3,- , -π中,最小的实数是( )A、1 B、-3 C、- D、-π3. 下列二次根式的运算正确的是( )A、+= B、=2 C、=±3 D、= -64. 在同一平面直角坐标系中,一次函数=a+1(a为常数,a<0)的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知a+b>0,ab>0,如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
 A、(a,b) B、(-a,b) C、(-a,-b) D、(a,-b)6. 已知(-3,y1),(1,y2),(-1,y3)都在直线y=3-b上,则下列关系式正确的是( )A、y1<y2<y3 B、y1<y3<y2 C、y2<y3<y1 D、y3<y1<y2
A、(a,b) B、(-a,b) C、(-a,-b) D、(a,-b)6. 已知(-3,y1),(1,y2),(-1,y3)都在直线y=3-b上,则下列关系式正确的是( )A、y1<y2<y3 B、y1<y3<y2 C、y2<y3<y1 D、y3<y1<y2二、填空题(共6小题,每小题3分,共18分)
-
7. 在平面直角坐标系中,一次函数y=+1的图象与y轴交点坐标为.8. m的平方根是±7,则m=.9. 已知点P1(a-1,5)和点P2(2,b-1)关于x轴对称,则(a+b)2023=.10. 《九章算术》中提出了如下问题:今有户不知高、广,竿不知长短,横之不出四尺,从之不出二尺,邪之适出,问户高、广、邪各几何?这段话的意思是:今有门不知其高宽;有竿,不知其长短,横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等。问门高、宽和对角线的长各是多少?则该问题中的门高是.11. 在平面直角坐标系中,将直线y=2+4沿向右平移2个单位长后,得到新直线的函数关系式为.12. 如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以每秒1cm的速度运动,设运动时间为t秒.当t为时,△ACP是等腰三角形.

三、解答题(本大题共5小题,每小题6分共30分)
-
13. 计算:(1)、-(2)、∣1∣14. 计算:(1)、+(2)、(2+)(2-)+15. 如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图:
 (1)、在图中画一条线段MN,使M=;(2)、在图中画一个三边长均为无理数,且各边都不相等的直角△DEF.16. 已知点P(2a-3,a+6),解答下列各题.(1)、点P在轴上,求出点P的坐标;(2)、若点P在第二象限,且它到轴、轴的距离相等,求a2003+2024的值.17. 已知某正数的两个平方根分别是a-3和2a+15,的立方根是-3.是的整数部分,求+-2的平方根.
(1)、在图中画一条线段MN,使M=;(2)、在图中画一个三边长均为无理数,且各边都不相等的直角△DEF.16. 已知点P(2a-3,a+6),解答下列各题.(1)、点P在轴上,求出点P的坐标;(2)、若点P在第二象限,且它到轴、轴的距离相等,求a2003+2024的值.17. 已知某正数的两个平方根分别是a-3和2a+15,的立方根是-3.是的整数部分,求+-2的平方根.四、解答题(共3小题,每小题8分,共24分)
-
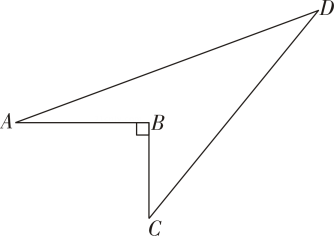
18. 如图,一块草坪的形状为四边形 , 其中 , , , , 求这块草坪的面积.
 19. 如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:
19. 如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:碗的数量(只) 1 2 3 4 5 ······ 高度(cm) 4 5.2 6.4 7.6 8.8 ······ 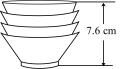 (1)、上述两个变量之间的关系中,哪个是自变量?哪个是因变量?(2)、用h(cm)表示这摞碗的高度,用(只)表示这摞碗的数量,请用含有的代数式表示h;(3)、若这摞碗的高度为11.2cm,求这摞碗的数量.20. 根据表格解答下列问题:
(1)、上述两个变量之间的关系中,哪个是自变量?哪个是因变量?(2)、用h(cm)表示这摞碗的高度,用(只)表示这摞碗的数量,请用含有的代数式表示h;(3)、若这摞碗的高度为11.2cm,求这摞碗的数量.20. 根据表格解答下列问题:x 13 13.1 13.2 13.3 13.4 13.5 13.6 13.7 13.8 13.9 14 x2 169 171.61 174.24 176.89 179.56 182.25 184.96 187.69 190.44 193.21 196 (1)、190.44的平方根是 .(2)、≈ , =.(3)、若13.5<<13.6,求满足条件的整数n的值.五、解答题(共2小题,每小题9分,共18分)
-
21. 如图,已知直线AB:=k+b与轴、轴分别交于A,B两点,且OA=2OB=8,轴上一点C的坐标为(6,0),P是直线AB上一点.
 (1)、求直线AB的函数表达式:(2)、连接OP和CP,当点P的横坐标为2时,求△COP的面积.22. 如图,长方形ABCD中,点E是AD的中点,将△ABE沿BE向下折叠后得到△GBE,将BG延长线交直线 DC于点F.
(1)、求直线AB的函数表达式:(2)、连接OP和CP,当点P的横坐标为2时,求△COP的面积.22. 如图,长方形ABCD中,点E是AD的中点,将△ABE沿BE向下折叠后得到△GBE,将BG延长线交直线 DC于点F. (1)、若点G恰好落在边BC上,则AD与AB的数量关系是.(2)、如果点G在长方形ABCD的内部,如图所示.
(1)、若点G恰好落在边BC上,则AD与AB的数量关系是.(2)、如果点G在长方形ABCD的内部,如图所示.①试探究线段BF,AB,DF之间的数量关系,并说明理由;
②若DF=DC,AD=8,求AB的长度.
六、解答题(本小题12分)
-
23. 在一条笔直的公路上有A、B两地,甲、乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动),甲、乙二人之间的距离(米)与出发时间(分钟)之间的函数关系如图所示,请结合图象解答下列问题:
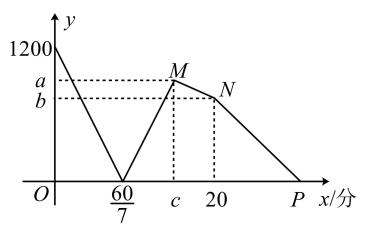 (1)、A、B两地之间的距离是米,乙的步行速度是米/分;(2)、求出a,b,c的值;(3)、求线段MN的函数解析式;(4)、在乙运动的过程中,何时两人相距80米?
(1)、A、B两地之间的距离是米,乙的步行速度是米/分;(2)、求出a,b,c的值;(3)、求线段MN的函数解析式;(4)、在乙运动的过程中,何时两人相距80米?