陕西省咸阳市2023-2024学年高三上学期1月高考分科调研模拟测试(二)理科数学试题
试卷更新日期:2024-01-12 类型:高考模拟
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知复数是纯虚数,则实数的值为( )A、±6 B、1或6 C、-6 D、12. 已知集合 , 若 , 则的子集有( )A、3个 B、4个 C、7个 D、8个3. 下列命题中,真命题是( )A、“”是“”的必要条件 B、 C、 D、的充要条件是4. 小张分别在A , B两个地块培育同一种树苗5棵,一周后观察它们的高度如图所示,则( )
 A、B地块树苗高度的众数小于A地块树苗高度的众数 B、B地块树苗高度的方差等于A地块树苗高度的方差 C、B地块树苗高度的平均值大于A地块树苗高度的平均值 D、B地块树苗高度的中位数等于A地块树苗高度的中位数5. 我国油纸伞的制作工艺非常巧妙.如图1,伞不管是张开还是收拢,伞柄始终平分同一平面内两条伞骨所成的角 , 且 , 从而保证伞圈能够沿着伞柄滑动.如图2,伞完全收拢时,伞圈已滑到的位置,且三点共线,为的中点,当伞从完全张开到完全收拢,半圈沿着伞柄向下滑动的距离为 , 则当伞完全张开时,的余弦值是( )
A、B地块树苗高度的众数小于A地块树苗高度的众数 B、B地块树苗高度的方差等于A地块树苗高度的方差 C、B地块树苗高度的平均值大于A地块树苗高度的平均值 D、B地块树苗高度的中位数等于A地块树苗高度的中位数5. 我国油纸伞的制作工艺非常巧妙.如图1,伞不管是张开还是收拢,伞柄始终平分同一平面内两条伞骨所成的角 , 且 , 从而保证伞圈能够沿着伞柄滑动.如图2,伞完全收拢时,伞圈已滑到的位置,且三点共线,为的中点,当伞从完全张开到完全收拢,半圈沿着伞柄向下滑动的距离为 , 则当伞完全张开时,的余弦值是( )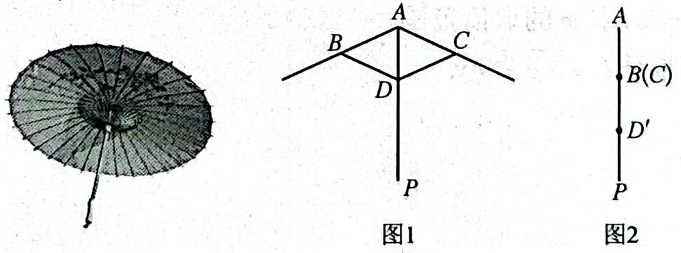 A、 B、 C、 D、6. 若 , 则( )A、 B、 C、 D、7. 已知为定义在上的奇函数,则函数的解析式可以为( )A、 B、 C、 D、8. 已知正四棱锥内接于表面积为的球 , 则此四棱锥体积的最大值为( )A、 B、 C、 D、9. 如图,在等腰梯形中,是线段上一点,且 , 动点在以为圆心,1为半径的圆上,则的最大值为( )
A、 B、 C、 D、6. 若 , 则( )A、 B、 C、 D、7. 已知为定义在上的奇函数,则函数的解析式可以为( )A、 B、 C、 D、8. 已知正四棱锥内接于表面积为的球 , 则此四棱锥体积的最大值为( )A、 B、 C、 D、9. 如图,在等腰梯形中,是线段上一点,且 , 动点在以为圆心,1为半径的圆上,则的最大值为( )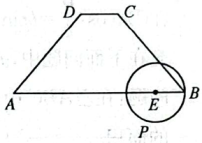 A、 B、 C、 D、10. 已知函数的零点为轴上的所有整数,则函数的图象与函数的图象的交点个数为( )A、8 B、9 C、10 D、1111. 设 , 则( )A、 B、 C、 D、12. 已知点是双曲线上位于第一象限内的一点,分别为的左、右焦点,的离心率和实轴长都为2,过点的直线交轴于点 , 交轴于点 , 过作直线的垂线,垂足为 , 则下列说法错误的是( )A、的方程为 B、点的坐标为 C、的长度为1,其中为坐标原点 D、四边形面积的最小值为
A、 B、 C、 D、10. 已知函数的零点为轴上的所有整数,则函数的图象与函数的图象的交点个数为( )A、8 B、9 C、10 D、1111. 设 , 则( )A、 B、 C、 D、12. 已知点是双曲线上位于第一象限内的一点,分别为的左、右焦点,的离心率和实轴长都为2,过点的直线交轴于点 , 交轴于点 , 过作直线的垂线,垂足为 , 则下列说法错误的是( )A、的方程为 B、点的坐标为 C、的长度为1,其中为坐标原点 D、四边形面积的最小值为二、填空题:本题共4小题,每小题5分,共20分.
-
13. 若函数是幂函数,且满足 , 则的值为.14. 如图,为平行四边形所在平面外一点,分别为上一点,且 , 当平面时,.
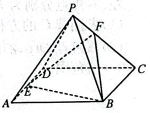 15. 已知正项等比数列中,成等差数列,其前项和为 , 若 , 则除以7的余数为.16. 如图,在平面直角坐标系中, , 圆过坐标原点且与圆外切,若抛物线与圆 , 圆均恰有一个公共点,则.
15. 已知正项等比数列中,成等差数列,其前项和为 , 若 , 则除以7的余数为.16. 如图,在平面直角坐标系中, , 圆过坐标原点且与圆外切,若抛物线与圆 , 圆均恰有一个公共点,则.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
-
17. 在①;②;③这三个条件中任选一个,补充在下面问题中,并给出解答.
问题:在中,角的对边分别为 , 且_▲_.求的面积.
注:如果选择多个条件分别进行解答,按第一个解答进行计分.
18. 如图,在三棱柱中,平面平面 , 侧面为菱形, , 是的中点.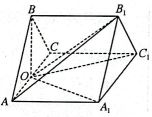 (1)、证明:;(2)、若二面角的余弦值为 , 求三棱柱的体积.19. 已知椭圆的离心率是双曲线的离心率的倒数,椭圆的左、右焦点分别为 , 上顶点为 , 且.(1)、求椭圆的方程;(2)、当过点的动直线与椭圆相交于两个不同点时,设 , 求的取值范围.20. 随着疫情时代的结束,越来越多的人意识到健康的重要性,更多的人走出家门,走进户外.近期文旅消费加速回暖,景区人流不息、酒店预订爆满、市集红红火火,旅游从业者倍感振奋.某乡村旅游区开发了一系列的娱乐健身项目,其中某种游戏对抗赛,每局甲获胜的概率为 , 乙获胜的概率为 , 两人约定其中一人比另一人多赢两局就停止比赛,每局比赛相互独立.设比赛结束时比赛进行的局数为.
(1)、证明:;(2)、若二面角的余弦值为 , 求三棱柱的体积.19. 已知椭圆的离心率是双曲线的离心率的倒数,椭圆的左、右焦点分别为 , 上顶点为 , 且.(1)、求椭圆的方程;(2)、当过点的动直线与椭圆相交于两个不同点时,设 , 求的取值范围.20. 随着疫情时代的结束,越来越多的人意识到健康的重要性,更多的人走出家门,走进户外.近期文旅消费加速回暖,景区人流不息、酒店预订爆满、市集红红火火,旅游从业者倍感振奋.某乡村旅游区开发了一系列的娱乐健身项目,其中某种游戏对抗赛,每局甲获胜的概率为 , 乙获胜的概率为 , 两人约定其中一人比另一人多赢两局就停止比赛,每局比赛相互独立.设比赛结束时比赛进行的局数为.求:
(1)、当时,甲赢得比赛的概率;(2)、的数学期望.附:当时,.