辽宁省五校联考2024届高三上学期期末数学考试
试卷更新日期:2024-01-12 类型:期末考试
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知 , 均为集合的子集, , , , 则( )A、 B、 C、 D、2. , 则的共轭复数等于( )A、 B、 C、 D、3. 若 , , 则( )A、 B、 C、 D、4. 的展开式中的系数为( )A、 B、 C、 D、5. 设 , , , 则的最小值为( )A、 B、 C、 D、6. 函数的部分图象如图,则( )
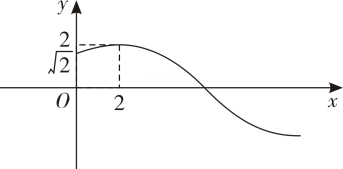 A、 , B、 , C、 , D、 ,7. 已知函数 , 设甲:;乙:是奇函数. 则( )A、甲是乙的充分条件但不是必要条件 B、甲是乙的必要条件但不是充分条件 C、甲是乙的充要条件 D、甲既不是乙的充分条件也不是乙的必要条件8. 圆锥曲线的发现与研究起源于古希腊,阿波罗尼奥斯(前262-前190)的《圆锥曲线论》全书8篇,共487个命题. 16世纪天文学和物理学揭示了圆锥曲线是自然界物体运动的普遍性形式. 17、18世纪随着射影几何学和解析几何学的创立发展,18世纪40年代瑞士数学家欧拉给出了现代形式下圆锥曲线的系统阐述. 现有圆锥顶点为 , 底面圆心为 , 母线与底面直径的长度相同. 点在侧面上,点在底面圆周上,为底面直径,二面角为. 已知平面与圆锥侧面的交线是某椭圆的一部分,则该椭圆的离心率为( )A、 B、 C、 D、
A、 , B、 , C、 , D、 ,7. 已知函数 , 设甲:;乙:是奇函数. 则( )A、甲是乙的充分条件但不是必要条件 B、甲是乙的必要条件但不是充分条件 C、甲是乙的充要条件 D、甲既不是乙的充分条件也不是乙的必要条件8. 圆锥曲线的发现与研究起源于古希腊,阿波罗尼奥斯(前262-前190)的《圆锥曲线论》全书8篇,共487个命题. 16世纪天文学和物理学揭示了圆锥曲线是自然界物体运动的普遍性形式. 17、18世纪随着射影几何学和解析几何学的创立发展,18世纪40年代瑞士数学家欧拉给出了现代形式下圆锥曲线的系统阐述. 现有圆锥顶点为 , 底面圆心为 , 母线与底面直径的长度相同. 点在侧面上,点在底面圆周上,为底面直径,二面角为. 已知平面与圆锥侧面的交线是某椭圆的一部分,则该椭圆的离心率为( )A、 B、 C、 D、二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的,全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 是随机变量,( )A、若 , 则 , B、若 , 则 C、若 , 则 , D、若 , 则10. 已知正方体的棱长为1,则( )A、直线与所成角的正弦值为 B、直线与平面所成角的正弦值为 C、点到直线的距离为 D、点到平面的距离为11. 已知点 , 在双曲线:上,点是线段的中点,则( )A、当时,点 , 在双曲线的同一支上 B、当时,点 , 分别在双曲线的两支上 C、存在点 , , 使得成立 D、存在点 , , 使得成立12. 已知函数 , 则( )A、当时,是的极小值 B、当时,是的极大值 C、当时, D、当时,
三、填空题:本题共4小题,每小题5分,共20分.
-
13. 已知向量 , , 且 , 则.14. 已知数列是首项为25,公差为的等差数列,则数列的前30项的和为.15. 在正三棱台中, , , , 则该棱台的体积为.16. 点在圆上,点在抛物线上,则线段长度的最小值为.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
-
17. 的内角 , , 的对边分别为 , , .已知.(1)、求;(2)、若 , 求.18. 为了解某药物在小鼠体内的残留程度,进行如下试验:随机抽取100只小鼠,给服该种药物,每只小鼠给服的药物浓度相同、体积相同. 经过一段时间后用某种科学方法测算出残留在小鼠体内药物的百分比. 根据试验数据得到如下直方图:
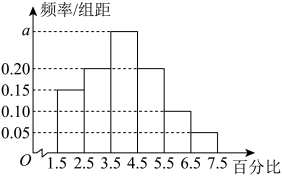 (1)、求残留百分比直方图中的值;(2)、估计该药物在小鼠体内残留百分比的平均值(同一组中的数据用该组区间的中点值为代表);(3)、在体内药物残留百分比位于区间的小鼠中任取3只,设其中体内药物残留百分比位于区间的小鼠为只,求的分布列和期望.19. 如图,在平行六面体中, , , , , 点为中点.
(1)、求残留百分比直方图中的值;(2)、估计该药物在小鼠体内残留百分比的平均值(同一组中的数据用该组区间的中点值为代表);(3)、在体内药物残留百分比位于区间的小鼠中任取3只,设其中体内药物残留百分比位于区间的小鼠为只,求的分布列和期望.19. 如图,在平行六面体中, , , , , 点为中点.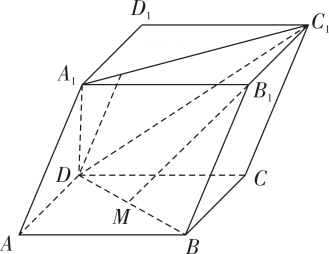 (1)、证明:平面;(2)、求二面角的正弦值.
(1)、证明:平面;(2)、求二面角的正弦值.