湖北省部分市州2023-2024学年高三上学期元月期末联考数学试卷
试卷更新日期:2024-01-12 类型:期末考试
一、单选题:每小题5分,共40分.每小题给出的四个选项中,只有一项是符合要求的
-
1. 已知为虚数单位,则( )A、 B、 C、-1 D、1
2. 定义全集 , 则( )A、 B、 C、 D、3. 设命题:数列是等比数列,命题:数列和均为等比数列,则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 已知任何大于1的整数总可以分解成素因数乘积的形式,且如果不计分解式中素因数的次序,这种分解式是唯一的.如 , 则2000的不同正因数个数为( )A、25 B、20 C、15 D、12
5. 某校高一年级有1200人,现有两种课外实践活动供学生选择,要求每个同学至少选择一种参加.统计调查得知,选择其中一项活动的人数占总数的60%到65%,选择另一项活动的人数占50%到55%,则下列说法正确的是( )A、同时选择两项参加的人数可能有100人 B、同时选择两项参加的人数可能有180人 C、同时选择两项参加的人数可能有260人 D、同时选择两项参加的人数可能有320人6. 圆锥中,为圆锥顶点,为底面圆的圆心,底面圆半径为3,侧面展开图面积为 , 底面圆周上有两动点 , 则面积的最大值为( )A、4 B、 C、 D、6
7. 抛物线的方程为 , 过点的直线交于两点,记直线的斜率分别为 , 则的值为( )A、-2 B、-1 C、 D、8. 已知函数 , 则下列关于说法正确的是( )A、的一个周期为 B、在区间上单调递减 C、的图象关于点中心对称 D、的最小值为二、多选题:每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对得5分,部分选对得2分,有错选得0分.
-
9. 新能源汽车相比较传统汽车具有节能环保、乘坐舒适、操控性好、使用成本低等优势,近几年在我国得到越来越多消费者的青睐.某品牌新能源汽车2023年上半年的销量如下表:
月份
1
2
3
4
5
6
销量(万辆)
11.7
12.4
13.8
13.2
14.6
15.3
针对上表数据,下列说法正确的有( )
A、销量的极差为3.6 B、销量的分位数是13.2 C、销量的平均数与中位数相等 D、若销量关于月份的回归方程为 , 则10. 已知圆与轴交于(原点),两点,点是圆上的动点, , 则( )A、的最大值为 B、的最小值为1 C、 D、令 , 则存在两个不同的点 , 使11. 设 , 点是直线上的任意一点,过点作函数图象的切线,可能作( )A、0条 B、1条 C、2条 D、3条12. 如图,某工艺品是一个多面体 , 点两两互相垂直,且位于平面的异侧,则下列命题正确的有( ) A、异面直线与所成角的余弦值为 B、当点为的中点时,线段的最小值为 C、工艺品的体积为 D、工艺品可以完全内置于表面积为的球内
A、异面直线与所成角的余弦值为 B、当点为的中点时,线段的最小值为 C、工艺品的体积为 D、工艺品可以完全内置于表面积为的球内三、、填空题:每小题5分,共20分.
-
13. 已知函数是偶函数,则.14. 若角的顶点在原点,始边与轴的非负半轴重合,终边与单位圆交于点 , 则.15. 已知方程有唯一实根,则实数的取值范围是.16. 设椭圆的左右顶点分别为为椭圆上异于的任意一点.过右焦点作轴的垂线与椭圆在第一象限交于点 , 连接并延长交直线于点 , 若 , 且 , 则椭圆离心率的取值范围是.
四、解答题:共70分.解答题需要在答题卡上写出必要的说明或推理过程.
-
17. 如图,在中, , 点是边上一点,且 ,
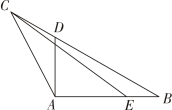 (1)、求的面积;(2)、求线段的长.18. 如图,在多面体中,底面为菱形,平面 , , 且为棱的中点,为棱上的动点.
(1)、求的面积;(2)、求线段的长.18. 如图,在多面体中,底面为菱形,平面 , , 且为棱的中点,为棱上的动点.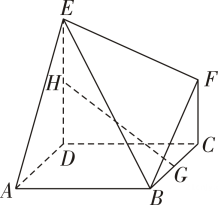 (1)、求二面角的正弦值;(2)、是否存在点使得平面?若存在,求的值;否则,请说明理由.19. 第19届亚运会于2023年9月23日至2023年10月8日在杭州举行.这是中国为世界呈现的体育盛会,也是亚洲人民携手写就的崭新篇章.现有某场乒乓球比赛采用5局3胜制,先赢3局的一方获胜,比赛结束.若参加比赛的甲每局比赛战胜对手乙的概率均为.假设各局比赛结果相互独立.(1)、求比赛恰好进行4局甲获胜的概率;(2)、设比赛进行的总局数为 , 求的分布列和数学期望;(3)、如果某场比赛赛前有3局2胜制和5局3胜制两种方案供选手选择,从概率角度考虑,乙如何选择对自己有利?请直接写出选择方案.
(1)、求二面角的正弦值;(2)、是否存在点使得平面?若存在,求的值;否则,请说明理由.19. 第19届亚运会于2023年9月23日至2023年10月8日在杭州举行.这是中国为世界呈现的体育盛会,也是亚洲人民携手写就的崭新篇章.现有某场乒乓球比赛采用5局3胜制,先赢3局的一方获胜,比赛结束.若参加比赛的甲每局比赛战胜对手乙的概率均为.假设各局比赛结果相互独立.(1)、求比赛恰好进行4局甲获胜的概率;(2)、设比赛进行的总局数为 , 求的分布列和数学期望;(3)、如果某场比赛赛前有3局2胜制和5局3胜制两种方案供选手选择,从概率角度考虑,乙如何选择对自己有利?请直接写出选择方案.