黑龙江省牡丹江市普通高中第二共同体2023-2024学年高三上学期1月期末联考数学试题
试卷更新日期:2024-01-12 类型:期末考试
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 已知集合的一个必要条件是 , 则实数的取值范围为( )A、 B、 C、 D、2. 已知 , 下列说法正确的是( )A、的虚部为 B、 C、 D、3. 点到双曲线的一条渐近线的距离为( )A、 B、 C、 D、4. 7个人站成两排,前排3人,后排4人,其中甲乙两人必须挨着,甲丙必须分开站,则一共有( )种站排方式.A、672 B、864 C、936 D、10565. 已知圆锥的底面半径为4,其侧面展开图为一个四分之一圆,则该圆锥的母线长为( )A、12 B、14 C、16 D、186. ( )A、1 B、 C、 D、27. 已知点 , 动点满足 , 则的取值范围是( )A、 B、 C、 D、8. 已知函数的零点为a,函数的零点为b,则下列不等式中成立的是( )A、 B、 C、 D、
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 已知向量 , 若 , 则等于( )A、0 B、-1 C、1 D、-210. 如图,在正方体中, , 点分别在棱和上运动(不含端点),若 , 则下列说法正确的是( )
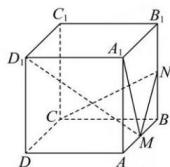 A、直线与直线所成角为 B、平面 C、 D、线段长度的最大值为11. 下列不等式正确的是( )A、已知为正实数, , 则的最小值为 B、有最小值2 C、已知正数满足 , 则的最大值是1 D、若对任意恒成立,则实数的取值范围是12. 已知抛物线 , 倾斜角为锐角的直线过其焦点并与抛物线交于两点 , 下列正确的是( )A、抛物线上的点到点的距离最小值为 B、三角形(为原点)面积最小值为 C、抛物线在点处的切线方程为 D、若 , 则
A、直线与直线所成角为 B、平面 C、 D、线段长度的最大值为11. 下列不等式正确的是( )A、已知为正实数, , 则的最小值为 B、有最小值2 C、已知正数满足 , 则的最大值是1 D、若对任意恒成立,则实数的取值范围是12. 已知抛物线 , 倾斜角为锐角的直线过其焦点并与抛物线交于两点 , 下列正确的是( )A、抛物线上的点到点的距离最小值为 B、三角形(为原点)面积最小值为 C、抛物线在点处的切线方程为 D、若 , 则三、填空题:本大题共4小题,每小题5分,共20分.
-
13. 某学校考试数学成绩服从正态分布 , 且 , 则成绩在的概率为 .14. 在正项等比数列中,已知 , 则 .15. 已知函数在上恰有两个零点,则的取值范围 .16. 函数有且只有3个零点,则实数的取值范围是 .
四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
-
17. 在中, .(1)、求;(2)、若 , 且的周长为 , 求的面积.18. 已知数列是递增的等差数列,数列是等比数列,且 , 、成等比数列, , ,(1)、求数列和的通项公式(2)、若 , 求数列的前n项和 .19. 近期,一些地方中小学生“课间10分钟”问题受到社会广泛关注,国家号召中小学要增加学生的室外活动时间.但是进入12月后,天气渐冷,很多学生因气温低而减少了外出活动次数.为了解本班情况,一位同学统计了一周(5天)的气温变化和某一固定课间该班级的学生出楼人数,得到如下数据:
温度(零下)
7
10
11
15
17
出楼人数
20
16
17
10
7
(1)、利用最小二乘法,求变量之间的线性回归方程;附:用最小二乘法求线性回归方程的系数:
(2)、预测当温度为时,该班级在本节课间的出楼人数(人数:四舍五入取整数).(3)、为了号召学生能够增加室外活动时间,学校举行拔河比赛,采取3局2胜制(无平局).在甲、乙两班的较量中,甲班每局获胜的概率均为 , 设随机变量X表示甲班获胜的局数,求的分布列和期望.