上海市闵行区2023-2024学年高一上学期1月学业质量调研（期末）数学试卷

试卷更新日期：2024-01-12 类型：期末考试

进入出卷网下载

一、填空题（本大题共有12题，满分54分，第1-6题每题4分，第7-12题每题5分）考生应在答题纸相应位置直接填写结果.

1. 设集合 $A = {0 ， 1 ， 2 ， 3 ， 4 ， 5} ， B = {x ∣ x \leq 1}$ ，则 $A \cap B =$ .

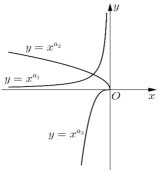
查看试题解析
2. 用有理数指数幂的形式表示 $\sqrt{\frac{a^{2}}{b^{3}}} =$ .（其中 $a > 0 ， b > 0$ ）

查看试题解析
3. 若 $x y = 1 (x ， y \in R)$ ，则 $x^{2} + y^{2}$ 的最小值为.

查看试题解析
4. 已知 $l o g_{2} 3 = a ， 2^{b} = 5$ ，则 $l o g_{2} 15 =$ .（用 $a ､ b$ 表示）

查看试题解析
5. 若函数 $y = e^{x} ， x \in [1 ， e]$ ，则此函数的最小值为.

查看试题解析
6. 已知 $f (x) = {\begin{array}{l} 2^{x - 2} ， x \geq 2 ， \\ \frac{1}{x - 2} ， x < 2 . \end{array}$ 若 $f (x_{0}) = 1$ ，则 $x_{0} =$ .

查看试题解析
7. 如图为三个幂函数 $y = x^{a_{1}} ， y = x^{a_{2}} ， y = x^{a_{3}}$ 在其定义域上的局部图像，则实数 $a_{1} ､ a_{2} ､ a_{3}$ 从小到大的排列顺序为.（请用“<”连接）

查看试题解析
8. 已知关于 $x$ 的不等式 $| x + 1 | + | x - a | \leq 5$ 有解，则实数 $a$ 的取值范围为.

查看试题解析
9. 已知 $y = f (x)$ 是定义在 $R$ 上的奇函数，且它在区间 $(- ∞ ， 0]$ 上是严格增函数，若不等式 $f (2 a - 3) + f (1 - a) < 0$ 成立，则实数 $a$ 的取值范围为.

查看试题解析
10. 在沪教版教材必修第一册第四章的章首语中有这样一段话：“通过固定等式 $a^{b} = c$ 中的三个量 $a ､ b ､ c$ 中的一个量，研究另两个量的相互关系和变化规律，定义三种基本而应用广泛的函数——幂函数､指数函数和对数函数”.若令 $c = e$ （ $e$ 是自然对数的底数），将 $a$ 视为自变量 $x (x > 0 ， x \neq 1)$ ，则 $b$ 为 $x$ 的函数，记作 $b = f (x)$ ，若不等式 $(x - 2 k) f (x) > 0$ 对任意的 $x \in (0 ， 1) \cup (1 ， + ∞)$ 恒成立，则实数 $k$ 的值为.

查看试题解析
11. 已知 $f (x) = 2^{x}$ ，若对任意的 $x_{1} \in [m ， n]$ ，存在唯一的 $x_{2} \in [m ， n]$ ，使得 $f (x_{1}) \cdot f (x_{2}) = 1$ ，则 $m + n$ 的值为.

查看试题解析
12. 将函数 $y = | x |$ 的图像绕原点逆时针方向旋转角 $α (0^{∘} < α < 36 0^{∘})$ ，在 $α$ 的变化过程中，每一个旋转角 $α$ 都对应一条折线，若该折线不是任何函数的图象，则 $α$ 的取值范围为.

查看试题解析

二、选择题（本大题共有4题，满分18分，第13-14题每题4分，第15-16题每题5分）每题有且只有一个正确选项.考生应在答题纸的相应位置，将代表正确选项的小方格涂黑.

13. 已知 $a ， b \in R$ ，则“ $a > 1 ， b > 1$ ”是“ $a b > 1$ ”的（）

A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分也非必要条件

查看试题解析
14. 下列函数中既是偶函数，又在区间 $(0 ， + ∞)$ 上是严格减函数的是（）

A、 $y = x^{\frac{2}{3}}$ B、 $y = \frac{1}{x^{2} + 1}$ C、 $y = l n | x |$ D、 $y = 2^{- x} - 2^{x}$

查看试题解析
15. 历史上数学计算方面的三大发明是阿拉伯数字､十进制和对数，其中对数的发明，大大缩短了计算时间，为人类研究科学和了解自然起了重大作用，对数运算对估算“天文数字”具有独特的优势.已知 $l g 2 \approx 0.301 ， l g 5 \approx 0.699$ ，则 $2 . 5^{2023}$ 的估算值为（）

A、 $1 0^{805}$ B、 $1 0^{806}$ C、 $1 0^{807}$ D、 $1 0^{808}$

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} l o g_{\frac{1}{2}} (1 - x) ， & - 1 \leq x \leq n ， \\ 2^{2 - | x - 2 |} - 2 ， & n < x \leq m \end{array} (n < m)$ 的值域是 $[- 1 ， 2]$ ，有下列结论：①当 $n = 0$ 时， $m \in [2 ， 4]$ ；②当 $n = \frac{3}{4}$ 时， $m \in (\frac{3}{4} ， 4]$ ；③当 $n \in [0 ， \frac{3}{4})$ 时， $m \in [2 ， 4]$ .其中正确结论的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

三、解答题（本大题共有5题，满分78分）解答下列各题必须在答题纸的相应位置写出必要的步骤.

17. 设集合 $A = {x ∣ | 2 x - 1 | < 3} ， B = {x ∣ x^{2} - (b + 1) x + b \leq 0}$ .

(1)、若 $b = 4$ ，试用区间表示集合 $A ､ B$ ，并求 $A \cup B$ ；

(2)、若 $B = [1 ， 5]$ ，求不等式 $\frac{b x + 1}{x - b} > 0$ 的解集.

查看试题解析
18. 已知 $f (x) = l o g_{2} (x + 1)$ .

(1)、解不等式 $f (x) < 1$ ；

(2)、判断函数 $y = f (2 x)$ 在其定义域上的单调性，并严格证明.

查看试题解析
19. 进口博览会是一个展示各国商品和服务的盛会，也是一个促进全球贸易和交流的重要平台.某汽车生产企业想利用2023年上海进口博览会这个平台，计划引进新能源汽车生产设备，通过市场分析，全年需投入固定成本3000万元，每生产 $x$ （百辆），需投入流动成本 $C (x)$ （万元），且 $C (x) = {\begin{array}{l} 10 x^{2} + 2000 x ， 0 < x < 28 ， \\ 2504 x + \frac{3600}{x} - 6400 ， x \geq 28 . \end{array}$ 其中 $100 x \in Z$ .由市场调研知道，每辆车售价25万元，且全年内生产的车辆当年能全部销售完.

(1)、写出年利润 $S (x)$ （万元）关于年产量 $x$ （百辆）的函数关系式；

(2)、年产量为多少百辆时，企业所获利润最大？并求出最大利润.
（总利润 $=$ 总销售收入-固定成本-流动成本 $)$

查看试题解析
20. 已知 $f (x) = \frac{a}{x} ， g (x) = x + b$ ，其中 $a ， b \in R$ .

(1)、判断函数 $y = | g (x) |$ 的奇偶性，并说明理由；

(2)、当 $a = 2$ 时，若函数 $y = f (x)$ 与 $y = | g (x) |$ 的图像有且只有三个公共点，求 $b$ 的取值范围；

(3)、记 $F (x) = f (x) + g (x)$ ，若函数 $y = F (x)$ 在区间 $(0 ， 2)$ 上有两个不同的零点，求 $b^{2} + 2 (b - a)$ 的取值范围.

查看试题解析
21. 已知函数 $y = f (x)$ 与 $y = g (x)$ 的定义域均为 $D$ ，若对任意的 $x_{1} ， x_{2} \in D (x_{1} \neq x_{2})$ 都有 $| g (x_{1}) - g (x_{2}) | < | f (x_{1}) - f (x_{2}) |$ 成立，则称函数 $y = g (x)$ 是函数 $y = f (x)$ 在 $D$ 上的“L函数”.

(1)、若 $f (x) = 3 x + 1 ， g (x) = x ， D = R$ ，判断函数 $y = g (x)$ 是否是函数 $y = f (x)$ 在 $D$ 上的“ $L$ 函数”，并说明理由；

(2)、若 $f (x) = x^{2} + 2 ， g (x) = \sqrt{x^{2} + a} ， D = [0 ， + ∞)$ ，函数 $y = g (x)$ 是函数 $y = f (x)$ 在 $D$ 上的“ $L$ 函数”，求实数 $a$ 的取值范围；

(3)、若 $f (x) = x ， D = [0 ， 2]$ ，函数 $y = g (x)$ 是函数 $y = f (x)$ 在 $D$ 上的“ $L$ 函数”，且 $g (0) = g (2)$ ，求证：对任意的 $x_{1} ､ x_{2} \in D (x_{1} \neq x_{2})$ 都有 $| g (x_{1}) - g (x_{2}) | < 1$ .

查看试题解析