吉林省长春市四十八中、二十九中、七十中2023-2024学年八年级上学期数学期末试卷
试卷更新日期:2024-01-12 类型:期末考试
一、选择题(每小题2分,共12分)
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若关于x的分式方程的解为非负数,则m的取值范围是( )A、且 B、且 C、且 D、且3. 如果点和点关于x轴对称,则的值是( ).A、 B、1 C、 D、54. 若一个三角形的三条边长分别为3,2a-1,6,则整数a的值可能是( )A、2,3 B、3,4 C、2,3,4 D、3,4,55. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A、108° B、90° C、72° D、60°6. 某次自然灾害导致某铁路隧道被严重破坏,为抢修其中一段120米的铁路,施工队每天比原计划多修5米,结果提前4天开通了列车,问原计划每天修多少米?某原计划每天修米,所列方程正确的是( )A、 B、 C、 D、
2. 若关于x的分式方程的解为非负数,则m的取值范围是( )A、且 B、且 C、且 D、且3. 如果点和点关于x轴对称,则的值是( ).A、 B、1 C、 D、54. 若一个三角形的三条边长分别为3,2a-1,6,则整数a的值可能是( )A、2,3 B、3,4 C、2,3,4 D、3,4,55. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A、108° B、90° C、72° D、60°6. 某次自然灾害导致某铁路隧道被严重破坏,为抢修其中一段120米的铁路,施工队每天比原计划多修5米,结果提前4天开通了列车,问原计划每天修多少米?某原计划每天修米,所列方程正确的是( )A、 B、 C、 D、二、填空题(每小题3分,共24分)
-
7. 因式分解: .8. 方程=-1的根为 .9. 若a2+a+1=2,则(5﹣a)(6+a)= .10. 如图所示,射线BA、CA交于点A,连接BC,已知AB=AC,∠B=40°,那么x的值是 .
 11. 如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有种.
11. 如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有种.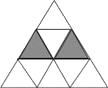 12. 如图,点在同一直线上, , 添加条件: , 则可用证明 .
12. 如图,点在同一直线上, , 添加条件: , 则可用证明 .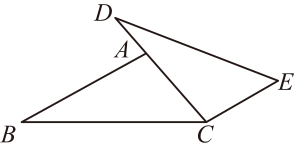 13. 如图,平分 , 点为上的任意一点, , 垂足为 , 线段的垂直平分线交于点 , 交于点 , 已知 , , 则的面积为 .
13. 如图,平分 , 点为上的任意一点, , 垂足为 , 线段的垂直平分线交于点 , 交于点 , 已知 , , 则的面积为 .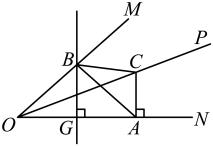 14. 已知一个长方形的长、宽分别为a,b,如果它的周长为10,面积为5,则代数式 的值为
14. 已知一个长方形的长、宽分别为a,b,如果它的周长为10,面积为5,则代数式 的值为三、解答题(每小题5分,共20分)
-
15. 分解因式: .16. 计算: .17. 解分式方程: .18. 已知:如图,C为BE上一点,点A、D分别在BE两侧,AB∥ED,AB=CE,BC=ED.
求证:AC=CD.

四、解答题(每小题7分,共28分)
-
19. 先化简: , 当时,请你为任选一个适当的数代入求值.20. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了四边形的两条边与 , 且四边形是一个轴对称图形,其对称轴为直线 .
 (1)、试在图中标出点 , 并画出该四边形的另两条边;(2)、将四边形向下平移3个单位,画出平移后得到的四边形 .21. 已知:如图,在中,
(1)、试在图中标出点 , 并画出该四边形的另两条边;(2)、将四边形向下平移3个单位,画出平移后得到的四边形 .21. 已知:如图,在中, (1)、作的平分线 , 交于点;作的中点(要求:尺规作图,保留作图痕迹,不必写作法和证明);(2)、连接 , 则 .22. 下面是小丽化简的过程,仔细阅读后解答所提出的问题.
(1)、作的平分线 , 交于点;作的中点(要求:尺规作图,保留作图痕迹,不必写作法和证明);(2)、连接 , 则 .22. 下面是小丽化简的过程,仔细阅读后解答所提出的问题.解:a(a+2b)﹣(a﹣1)2﹣2a
=a2+2ab﹣a2﹣2a﹣1﹣2a.第一步
=2ab﹣4a﹣1.第二步
(1)、小丽的化简过程从第几步开始出现错误;(2)、请对原整式进行化简,并求当a= , b=﹣6时原整式的值.五、解答题(每小题8分,共16分)
-
23. “佳园工艺店”打算制作一批有两边长分别是7分米,3分米,第三边长为奇数(单位:分米)的不同规格的三角形木框.(1)、要制作满足上述条件的三角形木框共有种.(2)、若每种规格的三角形木框只制作一个,制作这种木框的木条的售价为8元╱分米,问至少需要多少钱购买材料?(忽略接头)24. 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
 (1)、求证:△BCE≌△DCF;(2)、求证:AB+AD=2AE.
(1)、求证:△BCE≌△DCF;(2)、求证:AB+AD=2AE.六、解答题(每小题10分,共20分)
-
25. 某公司向甲、乙两所中学送水,每次送往甲中学7600升,乙中学4000升.已知人均送水量相同,甲中学师生人数是乙中学的2倍少20人.(1)、求这两所中学师生人数分别是多少;(2)、若送瓶装水,价格为1元/升;若用消防车送饮用水,不需购买,但需配送水塔,容量500升的水塔售价为520元/个,其他费用不计.请问这次乙中学用瓶装水花费少还是饮用消防车送水花费少?26. 如图,在直角三角形中, , 点D在射线上从点C出发向点A方向运动(点D不与点A重合),且点D运动的速度为 , 设运动时间为x秒时,对应的的面积为 .
 (1)、填写如表:
(1)、填写如表:时间x秒
…
2
4
6
…
面积y
…
…
(2)、在点D的运动过程中,出现为等腰三角形的次数有 次,请用尺规作图,画出(保留作图痕迹,不写画法);(3)、求当x为何值时,的面积是的面积的 .