湖南省永州市东安县五校联考2023-2024学年八年级上学期期中数学试题

试卷更新日期：2024-01-12 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，满分30分）

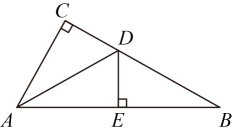
1. 下列式子： $- 5 x$ ， $\frac{1}{a + b}$ ， $\frac{1}{2} a^{2} - \frac{1}{2} b^{2}$ ， $\frac{3}{10 m}$ ， $\frac{2}{π}$ ，其中分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 若分式 $\frac{x}{3 - x}$ 有意义，则 $x$ 的取值范围是（）

A、 $x \leq 3$ B、 $x < 3$ C、 $x < 3$ 且 $x \neq 0$ D、 $x \neq 3$

查看试题解析
3. 把 $0.000000125$ 这个数据用科学记数法可表示为（）

A、 $0.125 \times 1 0^{- 7}$ B、 $1.25 \times 1 0^{- 6}$ C、 $1.25 \times 1 0^{- 7}$ D、 $0.125 \times 1 0^{- 8}$

查看试题解析
4. 下列运算正确的是（）

A、 $m^{2} \cdot m^{3} = m^{6}$ B、 $m^{6} \div m^{2} = m^{3}$ C、 $(m^{3})^{2} = m^{9}$ D、 $(m n)^{2} = m^{2} n^{2}$

查看试题解析
5. 把代数式 $\frac{x^{2} y}{x - y}$ 中的x，y同时扩大2倍后，代数式的值（）

A、扩大为原来的1倍 B、扩大为原来2倍 C、扩大为原来的4倍 D、缩小为原来的一半

查看试题解析
6. 在下列所给的四根已知长度的细木条中，能与长度为6cm，13cm的两根木条首尾相接钉成一个三角形木架的木条是（）

A、6cm B、7cm C、13cm D、20cm

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ，点E是斜边 $A B$ 的中点， $E D ⊥ A B$ ，且 $∠ C A D ： ∠ B A D = 5 ： 2$ ，则 $∠ B A C =$ （）

A、60° B、70° C、80° D、90°

查看试题解析
8. 下列命题中是真命题的是（）

A、同位角相等 B、过直线外一点有且仅有一条直线与已知直线平行 C、垂直于同一直线的两直线平行 D、三角形一边的中线平分三角形的周长

查看试题解析
9. 如图，在 $△ A C D$ 中， $∠ C A D = 90 °$ ， $A C = 5$ ， $A D = 12$ ， $A B ∥ C D$ ， E是 $C D$ 上一点， $B E$ 交 $A D$ 于点F，若 $A B = D E$ ，则图中阴影部分的面积为（）

A、30 B、48 C、50 D、60

查看试题解析
10. 如图，∠AOB=30°，OC为∠AOB内部一条射线，点P为射线OC上一点，OP=4，点M、N分别为OA、OB边上动点，则△MNP周长的最小值为（）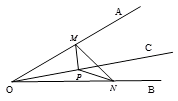

A、2 B、4 C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分）

11. 计算： ${(\frac{1}{2})}^{- 2} + {(- 2023)}^{0} =$ ．

查看试题解析
12. 计算 $a^{2} b {(a^{- 1} b)}^{- 2}$ =

查看试题解析
13. 如图，已知方格纸中鱼4个相同的正方形，则 $∠ 1 + ∠ 2 =$ ．

查看试题解析
14. 若等腰三角形的一个外角为70°，则它的底角为度．

查看试题解析
15. 如图，将Rt△ABC绕直角顶点C顺时旋转90°得到△A′B′C，连接AA′，若∠1=20°，则∠BAA′的度数为．

查看试题解析
16. 已知关于 $x$ 的方程 $\frac{x - 4}{x - 3} - k - 4 = \frac{k}{3 - x}$ 无解，则k的值为.

查看试题解析

三、解答题（本大题共9小题，满分72分）

17. 解方程： $\frac{x}{x - 1} = \frac{3 x}{2 - 2 x} + 1$

查看试题解析
18. 如图，已知 $△ A B C ≌ △ D B E$ ，点D在 $A C$ 上， $B C$ 与 $D E$ 交于点P．若 $∠ A B E = 160 °$ ， $∠ D B C = 30 °$ ，求 $∠ C B E$ 的度数．

查看试题解析
19. 甲、乙两辆汽车同时从 $A$ 地出发，开往相距200km的 $B$ 地，甲、乙两车的速度之比是4：5，结果乙车比甲车早30分钟到达 $B$ 地，求甲车的速度．

查看试题解析
20. 化简：

(1)、 $\frac{x}{x^{2} - 4} - \frac{1}{2 x - 4}$ ．

(2)、 $(1 - \frac{1}{a - 1}) \div \frac{a^{2} - 4 a + 4}{a^{2} - a}$

查看试题解析
21. 先化简，再求值： $1 - \frac{a^{2} + 2 a b + b^{2}}{a^{2} - a b} \div \frac{a + b}{a - b}$ ，其中 $a ， b$ 满足 $(a + 1)^{2} + | b + 1 | = 0$ ．

查看试题解析
22. 如图，点 $E$ 、 $F$ 在 $A B$ 上，且 $A E = B F$ ， $∠ C = ∠ D$ ， $A C / / B D$ ．求证： $C F // D E$ ．

查看试题解析
23. 有一块不规则的四边形木板ABCD，在BC边上有一点E，现在要在木板上找一点P，使点P到点A、点B的距离相等，并且PE∥AB．（要求：尺规作图，不写作法，保留作图痕迹）

查看试题解析
24. 我们已经学过 $(x - a) (x - b) = x^{2} - (a + b) x + a b ，$ 如果关于x的分式方程满足
$x + \frac{a b}{x} = a + b$ （a，b分别为非零整数），且方程的两个跟分别为 $x_{1} = a ， x_{2} = b$ ．
我们称这样的方程为“十字方程”．
例如： $x + \frac{2}{x} = 3$ 可化为 $x + \frac{1 \times 2}{x} = 1 + 2 = 3$ ∴ $x_{1} = 1 ， x_{2} = 2$
再如： $x + \frac{6}{x} = - 5$ 可化为 $x + \frac{(- 2) \times (- 3)}{x} = - 2 - 3 = - 5$ ∴ $x_{1} = - 2 ， x_{2} = - 3$
应用上面的结论解答下列问题：

(1)、“十字方程” $x + \frac{8}{x} = - 6$ ，则 $x_{1} =$ ， $x_{2} =$ ；

(2)、“十字方程” $x - \frac{2}{x} = - 1$ 的两个解分别为 $x_{1} = a ， x_{2} = b$ ，求 $\frac{1}{a} + \frac{1}{b}$ 的值；

(3)、关于 $x$ 的“十字方程” $x + \frac{n^{2} + n}{x - 3} = 2 n + 4$ 的两个解分别为 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，求 $\frac{x_{2}}{x_{1} + 1}$ 的值．

查看试题解析
25. 课外兴趣小组活动时，老师提出了如下问题：
如图1，在 $△ A B C$ 中，若 $A B = 12$ ， $A C = 8$ ，求 $B C$ 边上的中线 $A D$ 的取值范围．

小颖在组内经过合作交流，得到了如下的解决方法：如图2，延长 $A D$ 到点E，使 $D E = A D$ ，连接 $B E$ ，可证得 $△ A D C ≌ △ E D B$ ，即 $A C = B E$ ，请根据小颖的方法思考下列问题．

(1)、由“三角形的三边关系”可求得 $A D$ 的取值范围是．

(2)、解后反思：题目中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
完成上题之后，小颖善于探究，她又提出了如下的问题，请你解答．

如图3，在 $△ A B C$ 中，若 $A D$ 是 $△ A B C$ 的中线，E是 $A D$ 上一点，连接 $B E$ 并延长交边 $A C$ 于点F，且 $A F = E F$ ，求证： $A C = B E$ ．

(3)、如图4，在 $△ A B C$ 中，D是 $A C$ 的中点，分别以 $A B$ ， $B C$ 为直角边向 $△ A B C$ 外作等腰直角三角形 $A B M$ 和等腰直角三角形 $B C N$ ，其中 $∠ A B M = ∠ N B C = ∠ 90 °$ ，连接 $M N$ ，试探索 $B D$ 与 $M N$ 之间的数量与位置关系，并说明理由．

查看试题解析